Additionner avant de soustraire

L'addition se définit comme le regroupement des semblables : on a deux ensembles d'objets semblables, n pour le premier, m pour le second, on les regroupe,
et le regroupement a alors s = n + m objets.

Pour calculer s, le plus simple est de compter le nombre d'objets du regroupement, de la même façon qu'on a compté n et m dans les ensembles de départ.
Plus astucieusement, on peut partir de n et compter m en plus à partir de ce n pour trouver s, c'est ce que font les enfants en comptant sur leurs doigts.
Si on veut aller plus vite, et additionner des grands nombres, il faut trouver l'algorithme qui va prendre en compte les possibilités, et les contraintes, liées à la numération.

Pour cela, avec notre numération positionnelle et décimale, on a les règles suivantes :

• Ecrire les 2 nombres à additionner l'un sous l'autre, les unités sous les unités, les dizaines sous les dizaines et ainsi de suite;
• Partir de la droite, des unités,
  • Ajouter les chiffres des unités, si le total est inférieur à 10, inscrire ce total dans la ligne du résultat dans la colonne des unités
  • Si le total est supérieur à 10, enlever 10 et inscrire l'excédent dans la ligne du résultat dans la colonne des unités et RETENIR 1
• Passer aux dizaines et recommencer en prenant en compte la RETENUE si besoin
• Recommencer autant qu'il y a de chiffres au plus grand des nombres à Additionner

Avec cette méthode, il suffit d'apprendre les tables de l'addition de 1 + 1 = 2 jusqu'à 9 + 9 = 18 pour pouvoir faire toutes les additions des nombres aussi grands soient-ils.

Soustraire est-ce différent d'additionner ?...

La soustraction se définit souvent comme l'inverse de l'addition. En termes modernes,
si n + m = s , alors n = s - m , et de la même façon m = s - n.
En termes médiévaux,
la différence est ce qu'il conviendrait d'additionner à la quantité moindre pour retrouver la quantité majeure.

Deux difficultés viennent faire de la soustraction un exercice différent de l'addition.

• Alors que faire la somme de 2 nombres est toujours possible, la soustraction n'est possible que si le nombre à soustraire est plus petit que le premier nombre.
• Alors que l'algorithme de l'addition ne reporte la retenue que sur l'ordre de grandeur suivant,
  la soustraction peut conduire à des retenues en cascade, comme dans 1000 - 1 par exemple.

Ces deux différences se traduisent par une complexification de l'algorithme qui comprend les étapes suivantes :

• Ecrire les 2 nombres à soustraire l'un sous l'autre, les unités sous les unités, les dizaines sous les dizaines et ainsi de suite
• Vérifier que le premier est bien plus grand que le second (soit il a plus de chiffres, soit le premier chiffre qui diffère en partant de la gauche est supérieur)
• Partir de la droite, des unités
  • Si le chiffre à soustraire est plus petit, le soustraire et inscrire cette différence dans la ligne du résultat dans la colonne des unités
  • Si le chiffre à soustraire est plus grand, ajouter 10 au premier, soustraire le second et inscrire cette différence dans la ligne du résultat dans la colonne des unités et RETENIR 1
• Passer aux dizaines et recommencer en prenant en compte la RETENUE si besoin.
• Recommencer autant qu'il y a de chiffres au plus grand des nombres

Les 2 façons de poser la soustraction qui sont enseignées, et un challenger ...

Deux méthodes sont actuellement enseignées, la méthode "avec retenue" dite parfois française et la méthode "avec emprunt" ou "en cassant" dite parfois hollandaise.

La différence entre les deux méthodes porte sur la façon de dire et de faire les retenues.

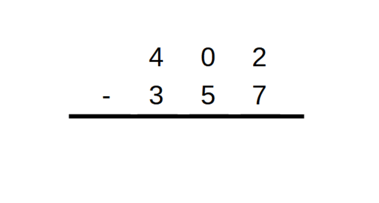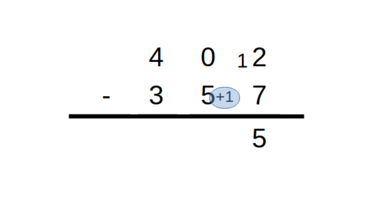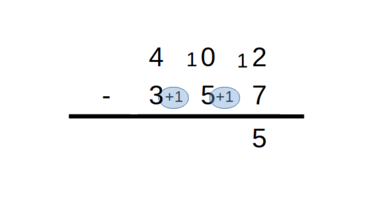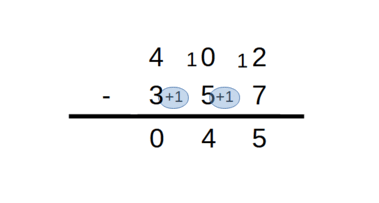
Dans la première, on est au plus proche de l'algorithme ci dessus. Reprenons l'exemple du manuscrit de Pamiers de 1430 (voir sur BNF Gallica ).
Soit à calculer 402 - 357 :
pour les unités, 2 est plus petit que 7, il faut donc rajouter 10, poser 5 unités et retenir 1 pour les dizaines,
pour les dizaines, 6 est plus petit que 0, il faut rajouter 10, puis poser 4 dizaines et retenir 1 pour les centaines,
et enfin 3 + 1 - 4 font 0 centaines
et le résultat est 45

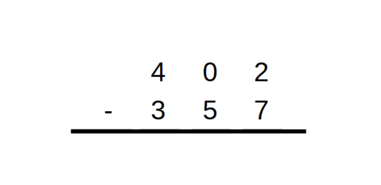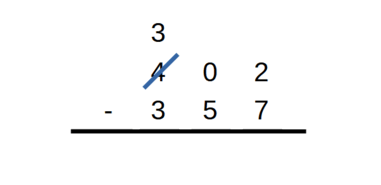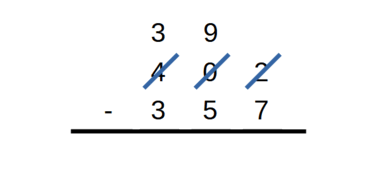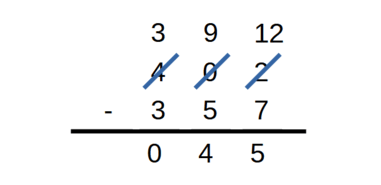
Dans la seconde méthode, on cherche à reproduire ce qu'on fait avec les supports matériels, jetons, abaques et bouliers : si on n'a pas assez d'unités on "casse" une dizaine.
Donc on fait directement -1 sur les dizaines du premier nombre, et, en même temps, plus 10 sur ses unités.
Mais s'il n'y a pas de dizaine (comme c'est le cas dans l'exemple) alors il faut aller "casser" une centaine, rajouter 9 dizaines et 10 unités !

Remarquons que cette méthode est peut-être plus facile à apprendre pour les petits nombres, en début d'apprentissage,
et qu'elle se raccorde mieux à la façon de faire avec les instruments comme les bouliers car, pour enlever des billes, il faut en avoir de disponibles.

Par ailleurs, et pour mémoire, le terme "emprunter" est aussi utilisé à la place de "casser".

Le challenger : le complément à 9

Les traités arithmétiques médiévaux n'acceptent pas les nombres négatifs comme nous le faisons aujourd'hui. La soustraction est donc un problème, et en particulier la retenue en cascade qui suppose de garder un -1 en retenue, même si on le maquille par un +1 dans le nombre à soustraire.

Un traité indien, Bhaskara (Lilavati) (1114-v. 1185), propose de résoudre ce point par la méthode du complément à 9, méthode qui sera présentée dans de mutiples traités d'arithmétique et, surtout, reprise au 17ème siècle par Pascal pour faire des soustraction mécaniquement sur sa Pascaline.

La méthode consiste à :

• Poser le nombre principal (par exemple 402)
• Prendre le complément à 9 du nombre à soustraire, ie on remplace chaque chiffre par 9 moins ce chiffre (pour 357 c'est 642)
• Ajouter ce complément à 9 au nombre principal (ici 402 + 642 = 1044)
• Retrancher 1000 et rajouter 1, le résultat est 45

Le calcul peut se détailler ainsi :
402 - 357 = 402 + 1000 - 1 - 357 - 1000 + 1 = 402 + (999 - 357) - 1000 + 1 = 402 + 642 - 1000 + 1

Avec cette méthode, plus besoin d'apprendre les tables de soustraction, seule celle de 9 est utile, et on s'épargne les retenues en cascade !