Diviser aujourd'hui en France et en Chine

La méthode pour la division n'a été stabilisée que tardivement, et elle reste encore différente d'un pays à l'autre. Prenons pour exemple la division : 6754 divisé par 357 donne 18 et il reste 328.

Voilà, à gauche comment elle se présente dans une école en France, et à droite dans une école en Chine.

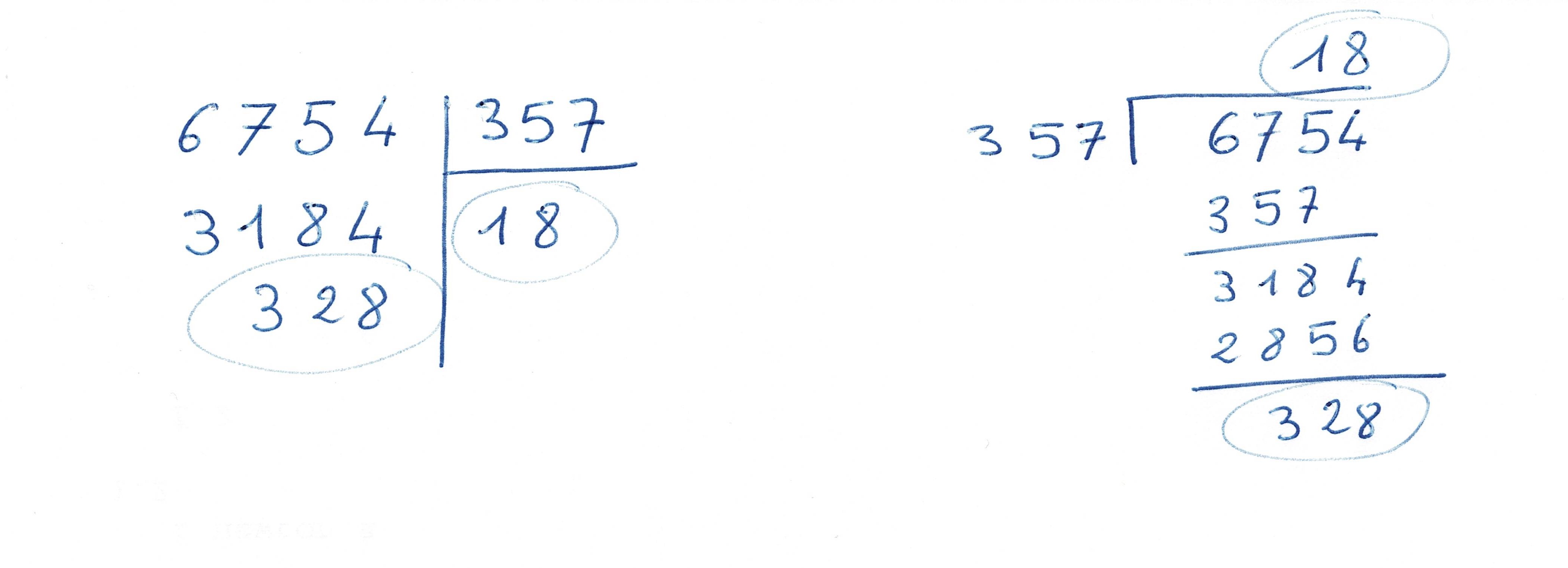
La division en galère

Reprenons cette division en vidéo comme elle est enseignée dans l'Arithmétique en sa perfection de Le Gendre. Cet ouvrage est un des classiques traités d'arithmétique dont la première édition date de 1648 et la dernière de 1820 ! Son concurrent était le traité de François Barreme dont le nom ne vous est pas inconnu. Le nom de division en galère vient de la forme en bateau qui reste sur la page une fois l'opération terminée.

Anecdote : lorsque Leibniz a travaillé sur la notation binaire, il s'est exercé à la division et, vers 1679, il utilisait la méthode de la division en galère, voilà ce que donne la division 1 / 6 (extrait de Leibniz on Binary de Strickland et Lewis, 2022). A gauche l'original manuscrit de Leibniz, à droite la transcription. Je vous laisse vérifier. Vous remarquerez que Leibniz n'utilise pas encore le signe " = " mais sa propre notation qui ressemble à pi.

La division égyptienne

La méthode égyptienne de multiplication avec la seule table de 2 présente l'avantage d'être pratiquement inversible et utilisable pour la division. Génial !

Remarque : notre méthode pour la division suppose de "deviner" au fur et à mesure les chiffres du diviseur. On peut considérer que ce n'est (presque) plus de l'arithmétique mais plutôt de l'algebre puisqu'il faut chercher le x tel que x fois le diviseur soit juste un peu inférieur au dividende. Par opposition, il n'y a rien à deviner avec la méthode égyptienne qui donne directement le résultat, vraiment arithmétique.

La division avec l'abaque de Gerbert

Gerbert d’Aurillac a été pape de 999 à 1003 sous le nom de Sylvestre II. Il a étudié l’arithmétique et tenté d’introduire dans l’occident chrétien les méthodes de calcul transmises par les arabes. Son élève Bernelin a écrit un ouvrage LIBRE d’ABAQUE dont la transcription en latin et la traduction en français ont été publiées sous ce titre en 2011. Bernelin y présente l’abaque de Gerbert d’Aurillac et comment l’utiliser pour faire des divisions simples ou complexes.

L’abaque comporte des colonnes pour les unités, les dizaines, les centaines, … et on place dans chaque colonne des jetons représentant les chiffres sur lesquels on opère.(source : IREM de la Réunion)

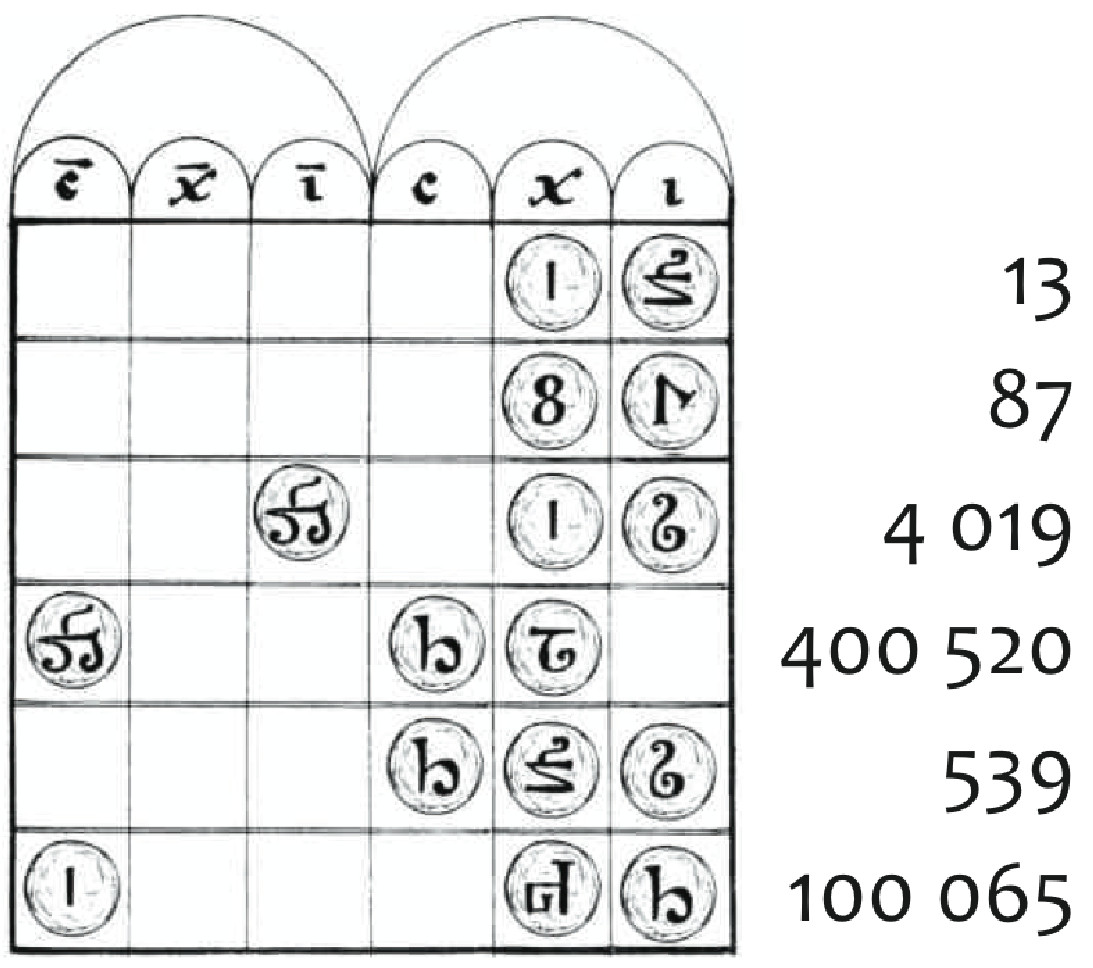On notera que Gerbert n’utilise pas de signe pour le zéro mais laisse la colonne vide et la graphie des chiffres qui vient des ouvrages arabes autour de l’an 1000. Pour plus de facilité, j’utilise la graphie moderne dans l’exemple ci-dessous.

Je reprends ici l’exemple de la division que j’ai déjà utilisé plus haut pour diviser "per galera" au XVIII ème siècle.

6754 divisé par 357 donne 18 et il reste 328.

La méthode dite de « division complexe avec différence » procède de la façon suivante.
Tout d’abord on trace un trait horizontal et sur ce trait on pose le dividende 6754 et au dessus le diviseur, 357.
Ensuite, au dessus du diviseur on pose le chiffre rond plus grand que le diviseur, ici 400 et, en dessous du diviseur, la différence entre 400 et 357, soit 43.
Le principe de la démarche est de diviser par un nombre plus grand mais plus facile à manier et de rajouter au reste le multiple de cette différence nécessaire.

On divise ensuite le chiffre des milliers, 6, par 4, soit 1 qu’on inscrit tout en bas de l’abaque, et reste 2 qu’on écrit juste sous le 6, on descend ensuite 754 et on rajoute 1 fois la différence soit 43 à l’aplomb du 1. En ajoutant les deux chiffres, le reste est donc de 3184 qui est plus petit que 3570, on peut donc passer aux unités.
On divise 31 par 4, soit 7, il reste 384 auquel il faut rajouter 7 fois 43 soit 301 et le reste est 685. Diviser 685 par 400 donne 1 avec un reste de 285 auquel il faut rajouter 1 fois la différence soit 43 et il reste à lire le résultat : la division donne 18 et un reste de 328.