Calculer à Sumer

Les Sumériens savaient calculer

Les tablettes mésopotamiennes donnent le résultat de calculs mais ne disent pas comment l'obtenir.
Elle ne donnent pas directement accès aux méthodes employées. Par contre, la richesse des résultats est étonnante.

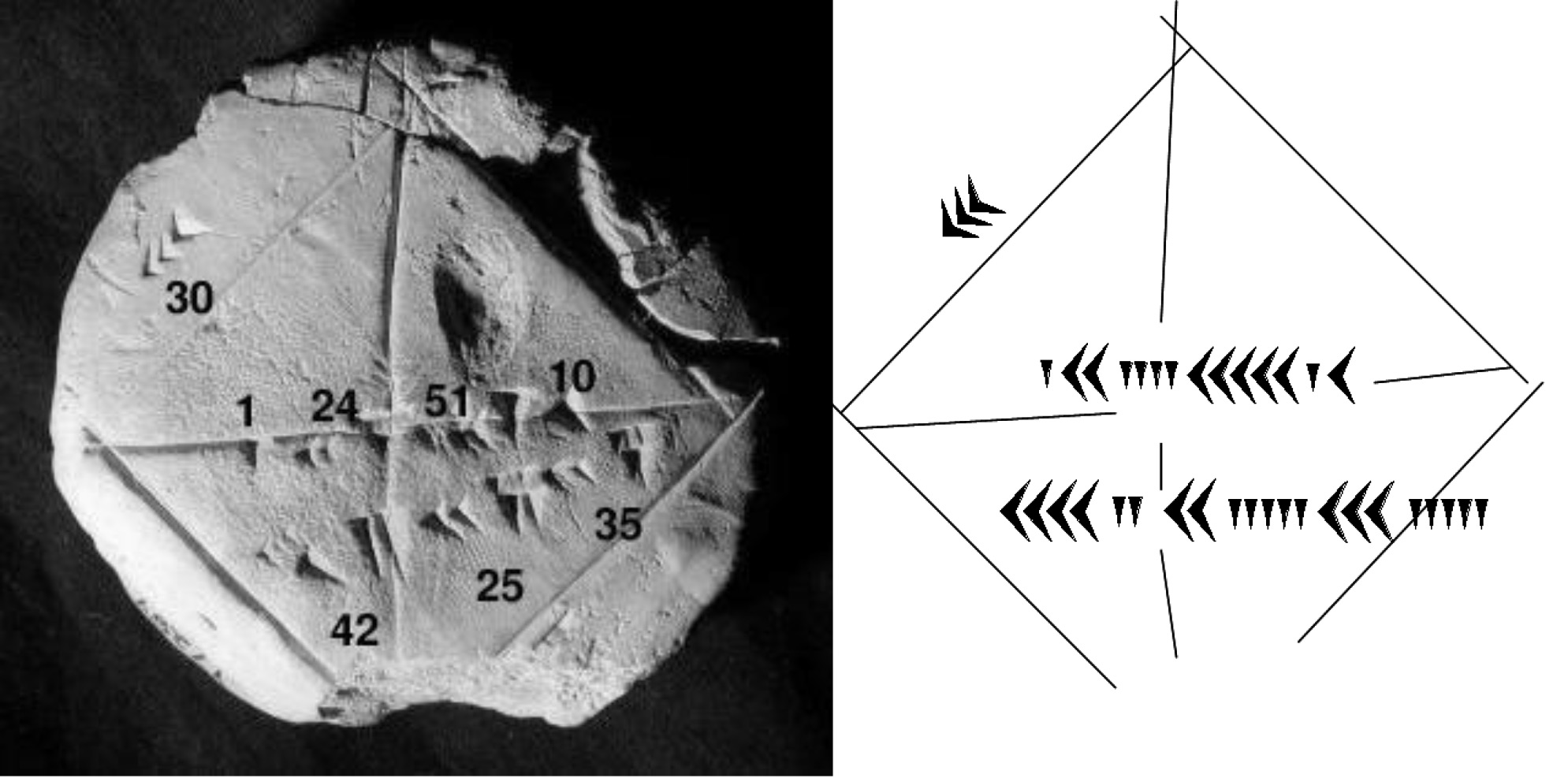
Cette tablette de Babylone réf.YBC 7289 (1900 avant JC) actuellement à Yale donne
la valeur de la racine de 2 calculée avec une précision de 4 10^-7
Noter que la notation ne précise pas l'ordre de grandeur (en base 60), avec plusieurs interprétations possibles de la seconde valeur : 1/racine(2), racine(2)/2 ou 60 fois cette valeur.
Des milliers de tablettes mathématiques ont été trouvées à Nippur incluant :
- des tables de multiplication, d’inverses, de carrés,
- des tables de transformation des bases de mesure (longueurs, surfaces, poids, volumes,...) vers la base de calcul et inversement.
Les tables d’inverses permettent de ramener la division à une multiplication. Ces tablettes sont souvent celles de scribes à l'école, elles montrent le niveau d'avancement de l'arithmétique mésopotamienne.

Multiplier avec la numération mésopotamienne (2000 ans avant JC)

Le système de numération des Mésopotamiens est proche du notre. C’est un système 'positionnel' où la valeur d’un chiffre dépend de l’endroit où il est placé.
Contrairement à nous qui écrivons les nombres avec 10 chiffres, de 1 à 9 et le 0, dans la base 10, les Sumériens utilisent la base 60 ou sexagésimale.
Ils ont deux "chiffres" (au sens de symbole élémentaire) le clou et le chevron, particulièrement bien adaptés à l'écriture avec un calame sur une tablette d'argile, puis ils écrivent les nombres de 1 à 59 en combinant ces symboles, ensuite ils passent à la puissance de 60 supérieure avec un clou qui vaut maintenant 60 au lieu de 1 et un chevron qui vaut 600 au lieu de 10.

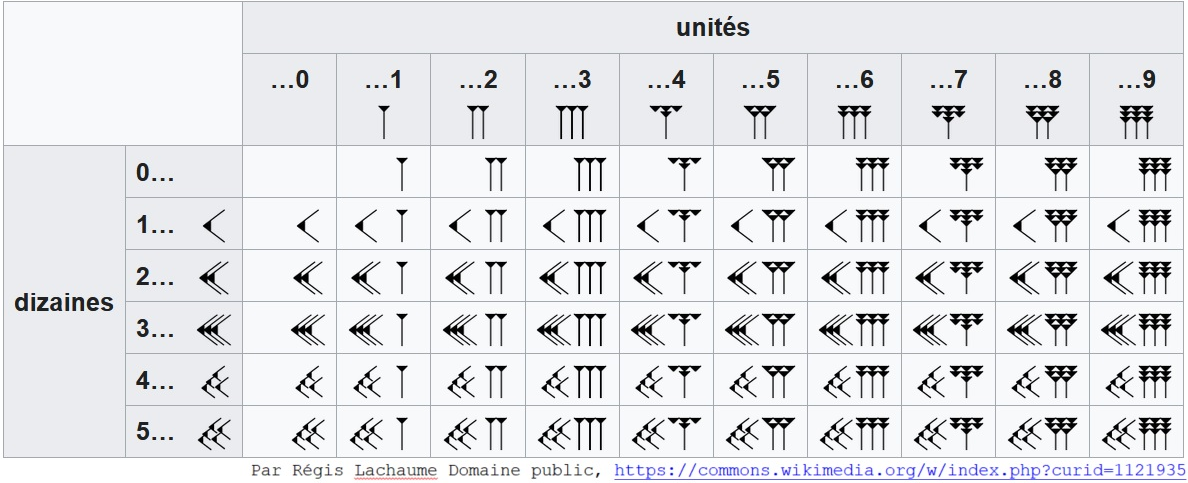
pour les unités, chaque clou vaut 1, et il y en a jusqu’à 9
chaque chevron vaut 10, il y en a jusqu’à 5.

Les Mésopotamiens utilisaient des tablettes en argile, de différentes tailles et différentes formes.
Ifrah p.368 donne l’exemple de la table de multiplication par 25 : une ligne de 1 à 20, puis une ligne pour 30,40 et 50.
La tablette ci-contre, conservée au Louvre est une table de multiplication par 44.26.40 soit 0,7407, et c'est également une table de division par 1,35. Cela représentait certainement un exercice intéressant pour les scribes, peut-être un résultat d'examen ?

On ne sait pas précisément comment les Sumériens multipliaient car on n'a pas de traces de calculs intermédiaires (cf. C. Proust).
Les tablettes dont nous disposons sont des supports pédagogiques, plutôt que des outils de travail. Il est probable que les Mésopotamiens connaissaient par coeur les tables de multiplication, comme aujourd'hui, mais avec 59 tables à apprendre au lieu de 9 !

L'attribut des scribes dans les représentations iconographiques est l'abaque, une planche en bois sur laquelle on étalait du sable et on écrivait les calculs intermédiaires avec un stylet en effacant au fur et à mesure de l'avancement du calcul (voir la multiplication par glissement ). C'est probablement ainsi que les scribes calculaient.
Ecrire des clous et chevrons sur un tel abaque n'est guère facile, les Mésopotamiens disposaient probablement d'une écriture cursive plus rapide et ne transposaient en clous et chevrons sur les tablettes que pour le résultat final.

Reprenons, notre multiplication : 365 x 76 ou 365,25 x 76 avec leur notation. Le scribe babylonien n'a certainement pas posé sa multiplication comme ici, mais on peut penser que le raisonnement soutendu ne lui était pas étranger.

365 = 6 *60 + 5 et s'écrit
76 = 1 *60 +16 et s'écrit
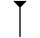on multiplie les unités 16 * 5
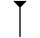puis les unités par les soixantaines 16 * 6
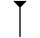puis les soixantaines par les unités 1 * 5
puis les soixantaines par les soixantaines 1 * 6
TOTAL

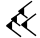
on peut convertir en base décimale pour vérifier : 7 * 3600 + 42*60 + 20 = 27740

Exercice : refaites le calcul avec les années bisextiles : 365,25 * 76

365,25 = 6 *60 + 5 + 15/60 et s'écrit
76 = 1 *60 +16 et s'écrit
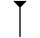vous trouverez le TOTAL

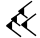
on peut convertir en base décimale pour vérifier : 7 * 3600 + 42*60 + 39 = 27759
mais, notez l'absence du zéro à droite et l'absence de virgule. En fait pour convertir en jours et en décimal on décide de placer la virgule ou l'unité en jours avant la dernière colonne.

La notation sexagésimale est donc utilisée pour faire les calculs et c'est au moment de la conversion en unités concrètes (de temps, de longueur, de surface, de poids, de monnaie, ...) que l'on fait le choix en fonction de l'ordre de grandeur.
Quand les systèmes d'unités sont différents selon ce qui est mesuré ou selon la région, le passage par un système sexagésimal unique est pratique pour multiplier, avant de revenir aux unités concrètes. Ce va et vient entre nombres concrets et nombres pour le calcul explique la présence de nombreuses tablettes spécifiques à la conversion.
Le système sexagésimal utilisé pour les multiplications peut aussi être envisagé comme flottant : un clou peut correspondre à 1, 60 ou 3600. Ca n'a pas d'importance car l'ordre de grandeur est inutile pour les multiplications. Les Sumériens n'ont donc besoin ni de la virgule, ni des zéros que nous mettons à droite des nombres pour préciser leur valeur absolue (1 10 100 1000 ou 0,1). Ce caractère flottant est une simplification et même un avantage selon C. Proust.

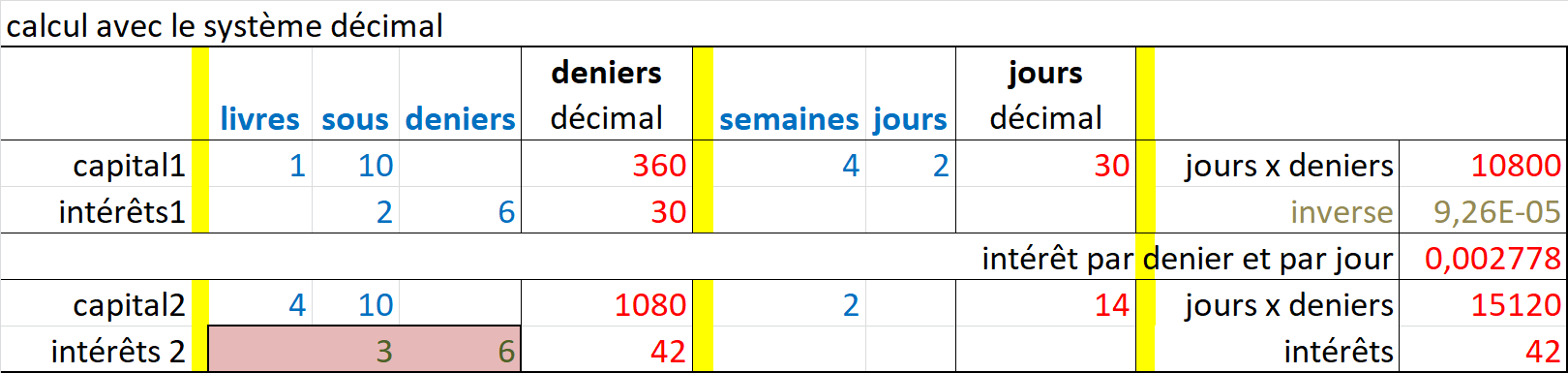
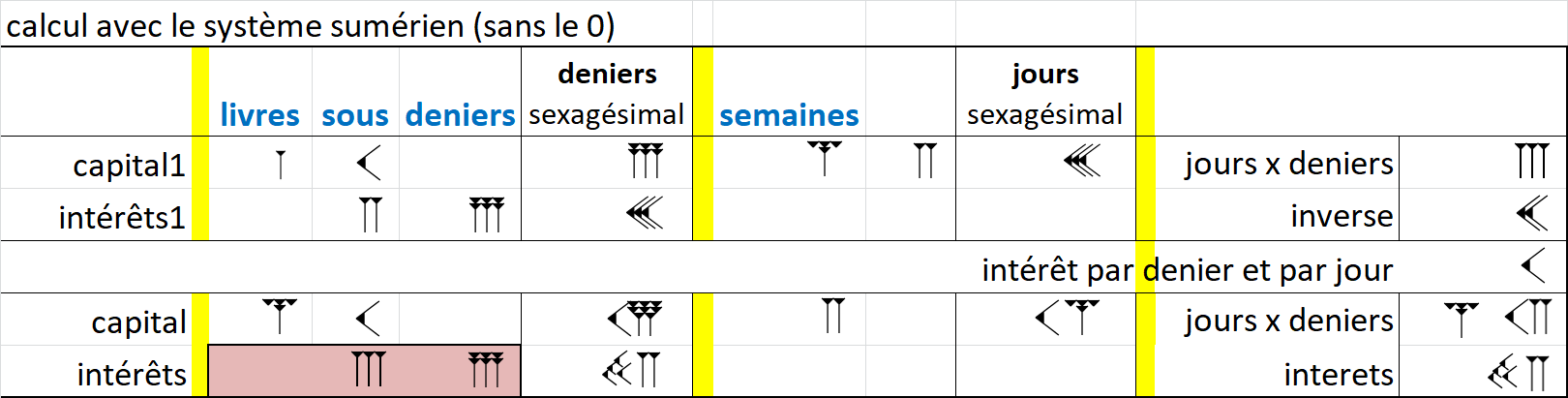
Exercice : examinez le problème suivant :
(sans remonter aux Mésopotamiens, il peut se poser depuis Charlemagne jusqu'à 1971 en Angleterre)

12 deniers font un sou et 20 sous font une livre,
sachant qu'une livre et 10 sous rapportent 2 sous et 6 deniers en 1 mois,
combien rapportent 4 livres et 10 sous en 2 semaines ?

Parions que, comme les Sumériens, pour faire le calcul, vous reviendrez vite à une notation plus amicale (par exemple en jours et en deniers) pour revenir aux unités de monnaie.

Solution : 3 sous et 6 deniers

Commençons par faire le calcul avec la numération décimale actuelle.

Les données initiales sont en bleu, les calculs en rouge et le résultat dans la zone colorée.

on convertit d'abord les livres, sous et deniers en deniers : pour trouver 360 et 1080 (colonne 5)
puis on convertit les durées de prêts en jours : pour trouver 30 et 14 (colonne 8)
et le produit de la durée du prêt par le montant : pour trouver 10800 et 15120 (dernière colonne)
l'intérêt correspondant au prêt d'un denier pendant un jour est donc de: 20/10800 = 0,002778 denier
on multiplie cet intérêt par denier et par jour par la durée et par le montant du 2° prêt pour trouver : 15120 * 0,002778 = 42 deniers
enfin, on reconvertit ces deniers en livres, sous et deniers pour trouver : 3 sous et 6 deniers

Reprenons ce même calcul avec la numération sumérienne (sans le 0 ni la virgule).

Prenez le temps de vous mettre à la place d'un scribe sumérien qui lit naturellement les symobles de 1

à 59

et qui connait par coeur ses tables de multiplication. Vous allez voir qu'il pourra faire le même calcul de tête, et bien plus vite que nous.

conversion des livres, sous et deniers en deniers : (colonne 5)
- livre à sous, plus sous font sous fois (12 deniers/sou) font deniers.
- livres à sous, plus sous font sous fois qui font deniers.
conversion des durées de prêts en jours : (colonne 8)
- semaines de jours, plus jours font jours (1 mois).
- semaines de jours font jours.
multiplier la durée du prêt par le montant : (dernière colonne)
- (le 1° montant) fois (la durée), égale
- (le 2° montant) fois (la durée), égale
Notez que le premier résulat est équivalent à 3 x 60 x 60 = 10800 (mais on n'a pas de zéro).
et que le deuxième résulat est équivalent à (4 x 60 + 12) x 60 = 15120.
calculer l'intérêt correspondant au prêt d'un denier pendant un jour,
- mais au lieu de diviser les intérêts payés (ou 30) par (ou 10800) comme on en décimal,
  on va, multiplier par l'inverse de soit (ou 20)
- donc fois égale (10).
Notez ici que l'intérêt par denier et par jour, est de (10), au lieu du 0,002778 obtenu en décimal!
mais c'est la même chose que 10 /(60*60) = 0,002778. La différence c'est que les sumériens font le calcul sans s'occuper de l'ordre de grandeur ou des zéros de droite.
On peut maintenant multiplier cet intérêt par jour et par denier ,
par la durée et le montant du 2° prêt :
- fois donne (42)
on va enfin re-convertir en livres, sous et deniers, mais on ne sait pas si le nombre à convertir est de 42 deniers, 42/60 de denier ou 42x 60 deniers. C'est le scribe qui va décider en fonction du bon sens et de l'ordre de grandeur.
Comme le 2° prêt est environ 3 fois plus élevé sur 2 fois moins de temps, le montant doit être du même ordre de grandeur, donc 42 deniers (plutôt que 42x60) ou 3 sous et 6 deniers.

Vous voyez qu'avec la numération sumérienne, le calcul est plus simple car on ne s'embarrase pas des ordres de grandeur pour les multiplications, par contre, il faut réfléchir à la fin pour savoir s'il faut mltiplier ou diviser par 60 avant de faire la conversion.
Vous voyez aussi que le taux d'intérêt est de 10 ou un chevron dans la notation sumérienne au lieu de 0, 00278 dans la notre. Mais le scribe sumérien sait très bien que ce taux correspond à 10/3600. Les autres taux 10/60 ou 10/216000 n'ayant pas de sens pour le commerce.

Page précédente