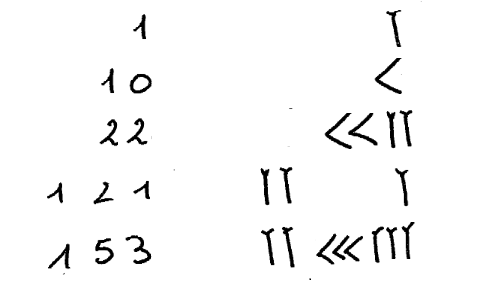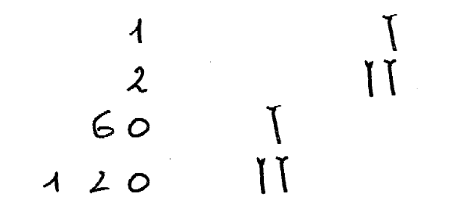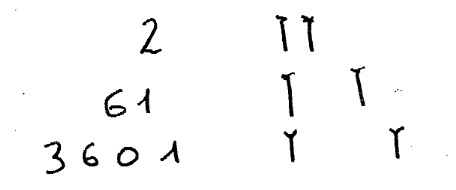Les débuts de l'aventure
compter énumérer représenter et écrire
à Sumer en Egypte à Rome ailleurs aujourd'hui
La préhistoire
Les humains calculaient avant d'écrire. Il est très difficile de savoir comment car il n'y a pas (ou très peu) d’outils de calcul dans les sépultures. On y trouve des bijoux, des armes, des symboles de la puissance et du rôle social, mais peu de traces du calcul.
Néanmoins, les marques sur certains objets sont interprétables comme l'enregistrement d'une quantité :
- L'os d'Ishango

Daté de 20000 ans BP, Congo, actuellement à Bruxelles.
Il est possible qu'un berger qui part avec un troupeau ait utilisé ces marques pour vérifier qu'il revient avec le même nombre de bêtes. Un curieux peut s'en servir pour compter les jours entre deux pleines lunes ou deux solstices. Et si tous les enfants posent la question rituelle "jusqu'à combien tu sais compter ?" , il est possible aussi que nos ancêtres préhistoriques se la soient posée.
Par ailleurs, sous toutes les latitudes, les humains utilisent leurs doigts et les autres parties du corps, pour compter.


Dans "l'histoire universelle des chiffres", Georges Ifrah décrit de multiples façons de compter avec les parties de son corps.
Exercice : dites ou montrez comment votre grand-mère compte sur ses doigts.
Exercice : Passez la souris sur les mains ci-dessous, pour qu'elles comptent jusqu'à 3, et dites si elles appartiennent à :
1. un Français,
2. un Japonais,
3. un Philippin,
4. un Chinois,
5. un Indien,
6. un citoyen de la Rome ancienne.
source Wikipedia






|
Compter sur ses doigts nous met en difficulté quand le nombre dépasse le nombre de doigts. Le plus facile est de passer au nombre de mains, puis au nombre de personnes. On avance naturellement vers ce que les mathématiciens appellent la base 10 : 34 correspond aux doigts de 3 personnes plus 4 doigts.
Enumérer puis dire les nombres
Les langues portent la trace du calcul préhistorique. Toutes permettent d'énumérer et dire des nombres avec une grande diversité (cf. Ifrah).
- diversité des mots, propres à chaque langue.
- diversité des bases : dizaine, douzaine, ...
qui peuvent se combiner : douze deniers font un sou et vingt sous font une livre,
et on peut dire quatre-vingt ou octante,... - diversité dans le plus grand nombre que l'on peut dire.
- les Grecs n'allaient pas plus loin que "myriade" qui valait 10 000 en notation moderne,
- et en Inde, le Mahaashankh vaut 10 puissance 19 (10 000 000 000 000 000 000).
- et diversité conceptuelle :
Au départ, les nombres ne se disent pas de la même façon selon ce qui est compté. Au lieu de deux, on peut dire un couple ou une paire.
On utilise des mots (milliers, millions, milliards, ...) pour désigner les grands nombres
ou des préfixes devant les unités (déca, hecto, kilo, mega) pour multiplier par 10, 100, 1000, 1 000 000... un décamètre, un hectolitre, un kilogramme, une mégatonne.
Dans les mots ou les préfixes que vous connaissez, quel est celui qui désigne le plus grand nombre ?
L'acquisition des nombres se fait avec des comptines comme "1 2 3 nous irons aux bois, 4 5 6 cueillir des cerises,...". Des 'comptines' pour apprendre à compter. Puis, une fois musique et paroles acquises, on accompagne du geste en comptant sur les doigts et on apparie les objets à compter avec la musique et le mouvement des doigts.
Représenter puis écrire les nombres
A Sumer, les transactions commerciales sont enregistrées avec des calculi (ou cailloux en latin), qui sont des jetons en pierre ou en terre cuite de différentes formes pour différentes valeurs.
Lorsqu'apparaît l'écriture, le dessin des calculi ou de ce qu'ils représentent devient la notation des nombres. Cette notation est même peut-être apparue avant l'écriture des mots (cf. Schmandt Besserat), la nécessité de préciser ce qui est compté y conduisant.
A Sumer, en Mésopotamie, on a retrouvé les traces d'un système de numération à base 10 et 60 (environ 5000 ans BP)

| Sumer, à Babylone bases 10 et 60 positionnelle | en Egypte base 10 | à Rome bases 5 et 10 | Les Incas (Quipus) | aujourd'hui base 10 positionnelle |
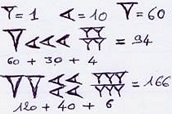
|

|

|

|
|
Notation des sumériens (Babylone)
Les Sumériens comptaient de 1 à 59 en base 10 puis utilisaient la base 60 (dite sexagésimale), comme on compte les minutes et secondes. L'astronomie grecque a hérité de l'astronomie mésopotamienne et a fait d'immenses progrès en conservant cette base sexagésimale.
Leurs chiffres de 1 à 59 sont des regroupements de symboles en forme de chevrons et de clous. Les chevrons valent 10 et on en met jusqu'à 5 et les clous valent 1, et on en met jusqu'à 9 :

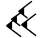

| vaut 42 (4 chevrons et 2 clous) |

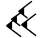

| vaut 342 avec, de gauche à droite, 5 clous, qui valent pour 5*60 =300, puis 4 chevrons pour 40 et 2 clous pour 2 |
(Voir wikipedia pour une description de cette notation sumérienne et voir Baptiste Meles pour un calculateur mésopotamien qui transcrit de notre base décimale à la leur et réciproquement !)
Les Mésopotamiens n'utilisaient ni le papier ni le papyrus. Ils écrivaient sur des tablettes d'argile à l'aide d'un calame (roseau). Les archéologues ont retrouvé des milliers de ces tablettes dont certaines sont des résultats d'exercices d'arithmétique.
A titre d'exemple, voici la table de multiplication par 8 en notation sumérienne qui pourrait faire l'objet d'une de ces tablettes sumériennes (réalisée par un scribe débutant du 21ème siècle) :

Exercice : écrire 2 puis 5, 10, 25, 59, 60 et 130 en notation sumérienne.
Un point fort de la notation en base 60 est de faciliter la division par 2 ou 3, 4, 5, 6 en remplacant la division par une multiplication, respectivement par 30, 20, 15, 12, 10 (mais ça ne marche pas pour 7 qui ne divise pas 60). Notre notation décimale, facilite la division par 2 et 5 (mais ça ne marche pas pour 3, qui n'est pas un divisieur de 10)
Cette notation a aussi ses difficultés: des nombres différents peuvent être écrits de la même manière
Exercice : écrire 1, 10, 22, 121 et 153 en notation sumérienne
Exercice : écrire 1, 2, 60, 61, 120 (en sumérien).
Avez vous une remarque ?
Exercice : écrire 2, 61 et 3601(en sumérien).
Avez vous une autre remarque ?
L'Egypte
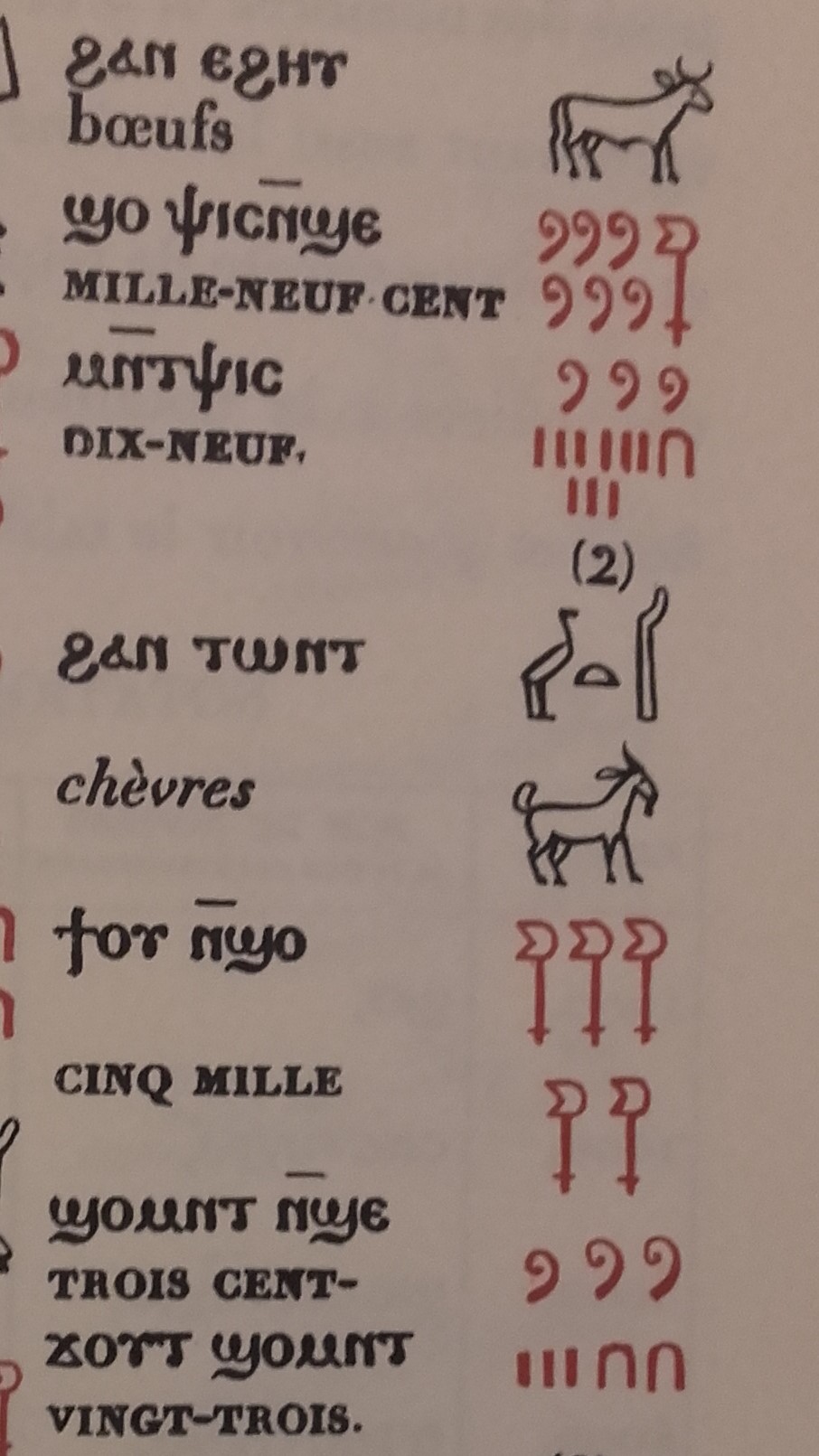
Avec les Egyptiens, on retrouve la base 10 mais leur écriture hiéroglyphique des nombres n'est pas positionnelle, il faut un nouveau symbole à chaque puissance de 10.
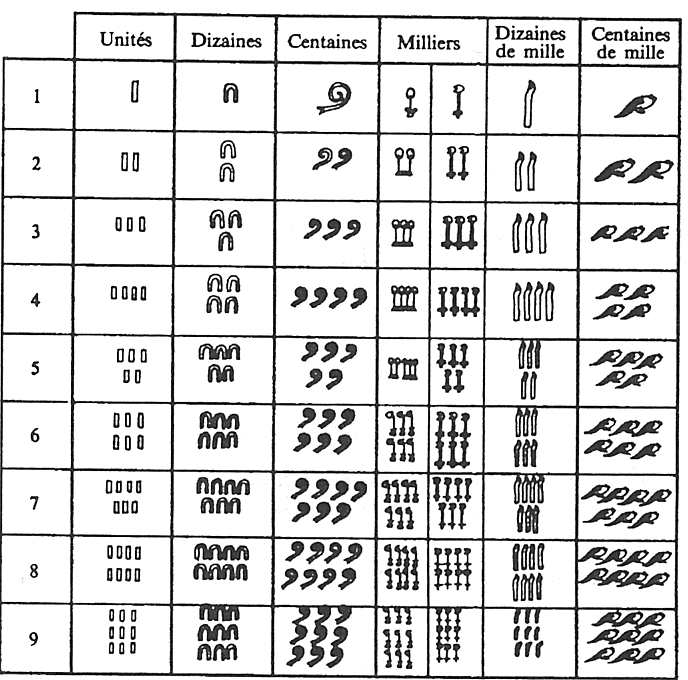
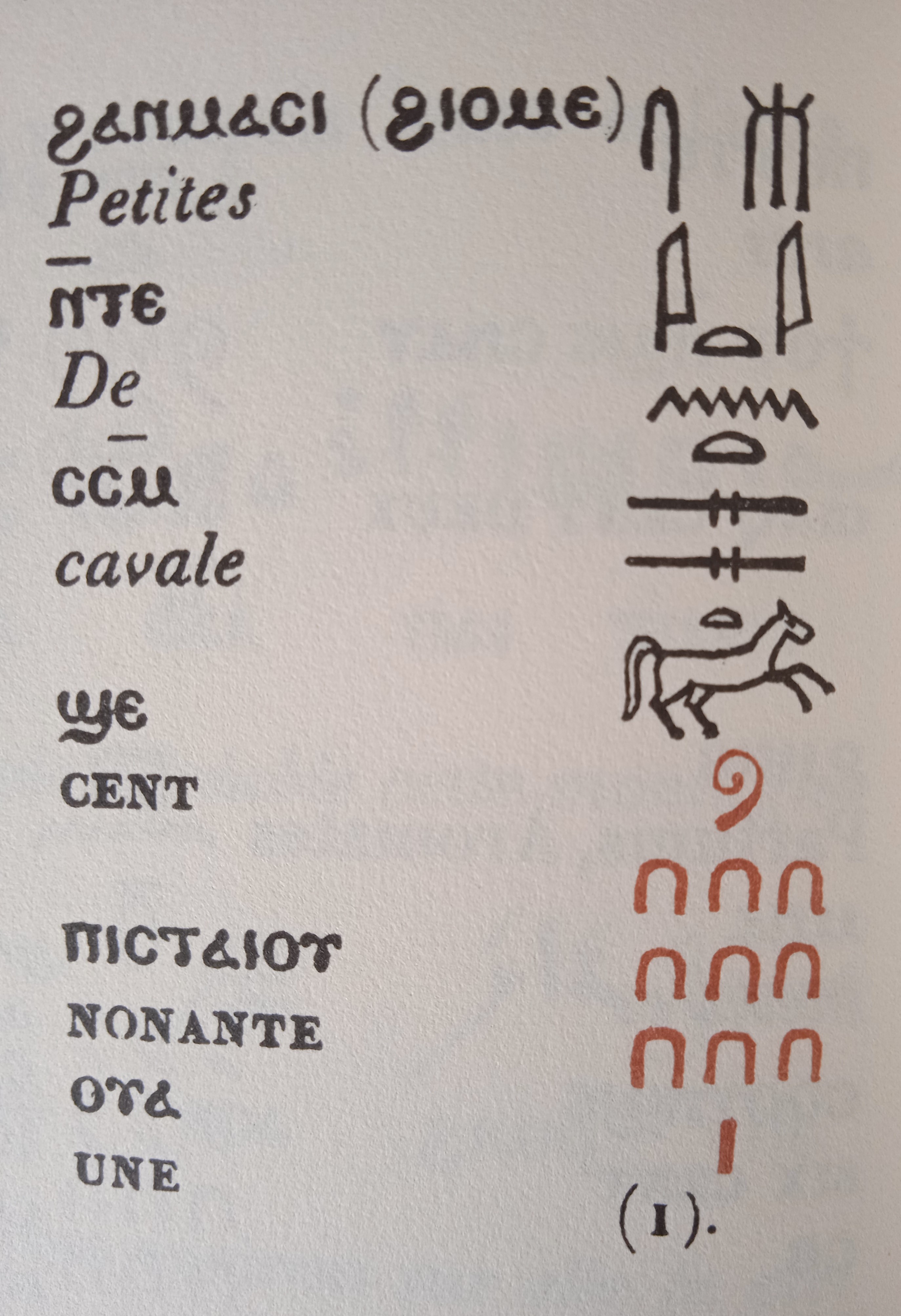
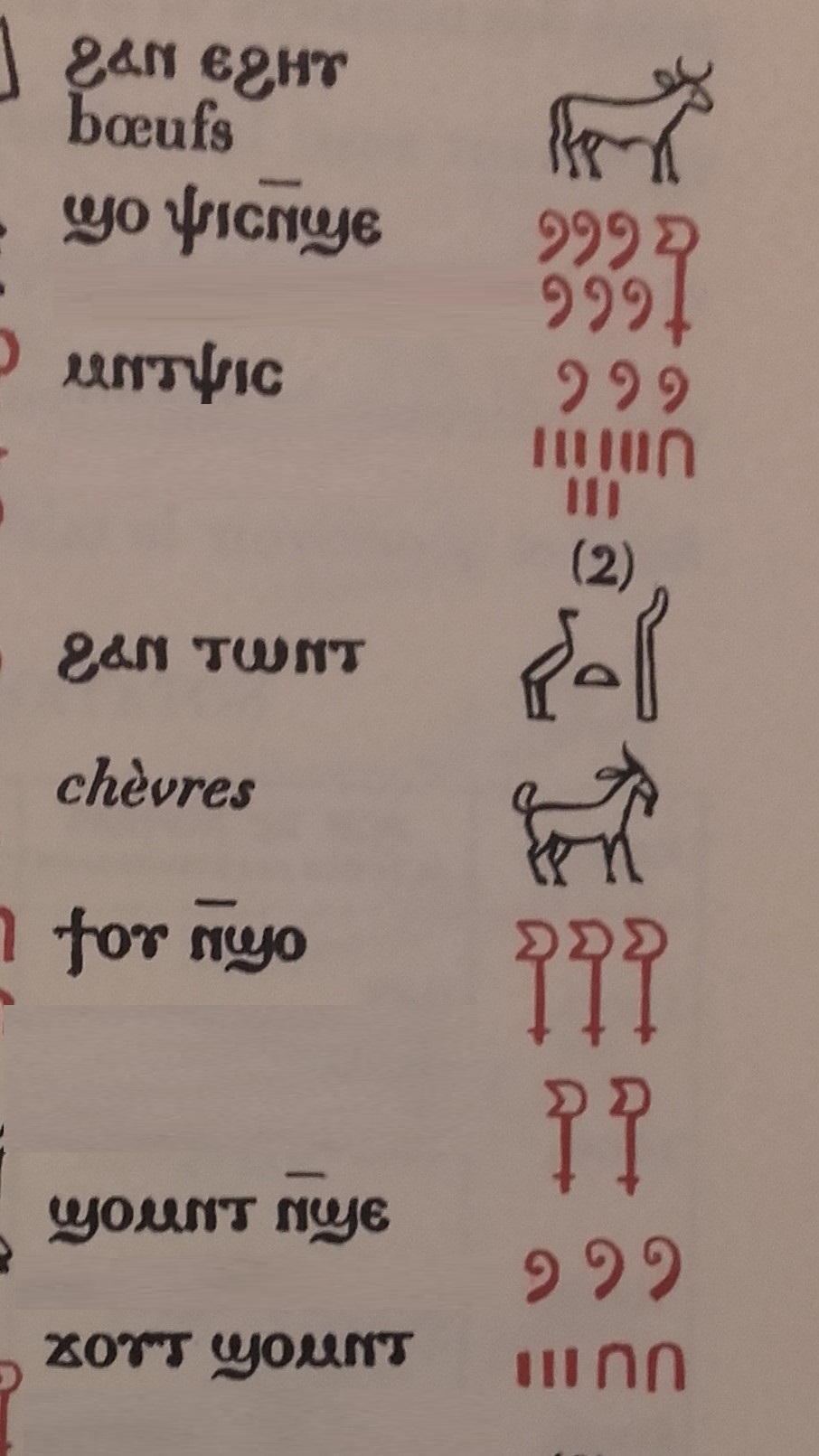
Dans les extraits ci-dessus, du livre de Champolion, vérifiez le nombre de chevaux sur la tablette du centre (191), puis lisez la tablette de droite.
Combien il y a de boeufs et de chèvres ?
Un avantage de la notation purement additive et non positionnelle est qu'elle marche en écrivant dans tous les sens, et c’est ce que faisaient les Egyptiens avec les hiéroglyphes (le sens en est donné par les figures humaines)
Voyons comment s'écrivent 61 et 101 en Mésopotamie, et en Egypte :

Les Egyptiens n’ont donc pas un besoin vital du zéro. Les Grecs et les Romains reprendront cette numération additive non positionnelle et n'auront pas non plus besoin du signe zéro. (cf.page suivante)
Grâce aux papyrus mathématiques, dont le célèbre papyrus de Rhind, on en sait beaucoup sur les opérations que faisaient les Egyptiens. Elles sont présentées dans la section "calcul à la plume". A noter que ces calculs ne s'appuyaient pas sur l'écriture hiéroglyphique des nombres, mais sur des écritures cursives plus efficaces.

Le monde romain
On passe au monde romain et à l’origine des bouliers.
- la numération est du même type que celle des Egyptiens. Elle est principalement décimale et non positionnelle.
- elle utilise 2 bases, 5 et 10, avec les symboles I V X L C D M pour 1 5 10 50 100 500 1000
- un nombre écrit en chiffres romains est facile à porter sur les abaques. On met un caillou qui vaut 1 sur la ligne I, 10 sur la ligne X et 5 entre les deux,
Exercice : écrire sur un abaque
dessinez un abaque comme celui-ci et placez 6 calculi pour écrire 365 ou CCCLXV
(vous pouvez utiliser des jetons, boutons, ... ou les dessiner au crayon.)

Pour les Grecs, les Romains, et ensuite pendant plus de 1000 ans pour tout le monde chrétien, le calcul va s'appuyer sur des jetons (ou cailloux : "calculi") manipulés sur des abaques. En même temps, dans le monde indien et dans le monde musulman, les calculs se font soit sur ces abaques soit en utilisant la puissance de la numération inventée par les Indiens : la numération décimale de position.
ailleurs : mondes incas et chinois
La base 10 est utilisée dans de nombreuses contrées, en Chine avec des baguettes qui remplacent les pierres, et chez les Incas avec les quipus et les yupanas, … et l'inventaire des historiens se limite aux cultures qui ont laissé des traces retrouvées et interprétées.


La numération moderne, décimale et positionnelle
Al Khwarizmi (qui par ailleurs invente l'Algèbre en prolongement de Diophante) publie vers 830 un ouvrage sur "le calcul indien". Cet ouvrage sera maintes fois repris et amplifié dans tout le monde arabe jusqu'en Espagne où de nombreuses versions seront traduites en latin.
Gerbert d'Aurillac, futur pape Sylvestre II, dit pape de l'an 1000, tentera sans succès d'introduire ces façons de calculer dans le monde chrétien. Ce n'est que 2 siècles plus tard avec Léonard de Pise que cette introduction deviendra, très progressivement, effective.
Voici comment en 1430 dans le compendi de l'art de l'algorisme, dit manuscrit de Pamiers, l'auteur décrit cette numération de position (texte en occitan, traduction (simplifiée) par Yves Serra pour onvaessayer.org) :
En suivant l’art d’Al Khwarizmi, voici comment noter tous les nombres. C’est à dire, comment regrouper les unités pour faciliter les comptes. On utilise 10 signes. D’abord 9 signes qui valent chacun pour leurs unités : Le premier est « 1 » et vaut pour une unité Le deuxième est « 2 » et vaut pour deux unités Et ainsi de suite « 3 4 5 6 7 8 9 » jusqu’à 9 qui vaut pour neuf unités Le dixième signe « 0 » est appelé zéro et ne vaut rien en lui-même mais permet de changer la signification des autres signes de la façon suivante : « 1 » vaut pour une unité « 10 » vaut pour une dizaine, ou dix unités « 20 » vaut pour deux dizaines, ou vingt unités et ainsi de suite jusqu’à « 90 » qui vaut pour neuf dizaines, ou quatre-vingt-dix unités « 100 » vaut pour une centaine, c’est à dire dix dizaines « 200 » vaut pour deux centaines, ou vingt dizaines et ainsi de suite jusqu’à « 900 » qui vaut pour neuf centaines Rajouter un zéro à droite change ainsi la signification du signe en compte soit d’unités, soit de dizaines, soit de centaines, et ainsi de suite, de façon qu’un zéro de plus à droite donne une valeur dix fois plus grande. On a donc trois façons de noter un nombre avec la méthode indienne : - la façon directe de 1 à 9, quand chaque signe vaut pour les unités qu’il représente - la façon des dizaines (et des centaines) quand chaque signe représente le nombre de dizaines (ou de centaines) selon le nombre de zéros qui sont à droite : 10, 20, .., 90, 100, 200, … 900 - la façon composée quand il y a à la fois des centaines, des dizaines et des unités, la position donnant la signification de chaque signe. Avec ces trois façons, on aura noté tous les nombres de 1 à 999. Ayant ainsi regroupé les unités à compter en unités, dizaines et centaines, on fera de même avec les milliers : « 1000 » , un millier, vaut pour dix centaines, cent dizaines ou mille unités, et on comptera ensuite les dizaines de milliers et les centaines de milliers. Et on aura ainsi compté jusqu’à « 999 999 » soit neuf cent quatre-vingt dix neuf mille neuf cent quatre-vingt dix neuf. On recommencera ensuite avec les millions, un million valant 10 centaines de milliers, ou mille milliers d’unités. Avec les dizaines de millions et les centaines de millions, on aura compté jusqu’à 999 999 999.
Et sur cette base de la numération décimale de position, l'ouvrage d'Al Khwarizmi développe comment faire toutes les opérations "à la plume" sans abaque ni jetons.