Numérations additives et positionnelles inventions des zéros

Numérations additives et positionnelles

Revenons sur les types de numération utilisées pour les comptes et les calculs. Elles se distinguent par la ou les bases utilisées: 2, 5, 10, 12, 20 et 60 et par leur caractère additif ou positionnel :

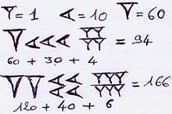
• dans une représentation additive, la valeur d'un chiffre ou d'un symbole est indépendante de sa position : c'est le cas de la numération égyptienne,
• dans une représentation positionnelle, la valeur d'un chiffre ou d'un symbole dépend de sa position : c'est le cas de la numération sumérienne et de la numération décimale actuelle.
• Les représentations peuvent être hybrides :
  * dans la notation romaine, le 4 est représenté par IV ou 5-1 plutôt que par IIII,
  * dans la notation sumérienne, les termes de 1 à 59 sont une addition de clous et chevrons, le 19 est souvent écrit comme 20-1.
  On peut néanmoins ranger la numération sumérienne comme positionnelle et la numération romaine comme additive.

L'écriture positionnelle simplifie l'utilisation des tables de multiplication :

pour nous la table de Pythagore, pour les calculs de nos grands parents des tables imprimées comme celles de le Pelletier pour des nombres à 3 et 2 chiffres, et pour les Sumériens les tablettes de multiplication en argile, de 1 à 20 et 30,40,50 que les scribes apprenaient par coeur.
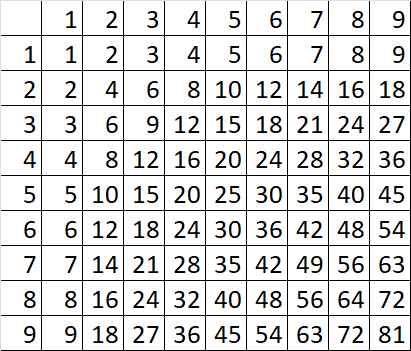
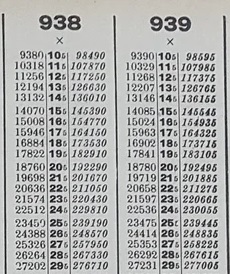
Avec ces tables, la numération positionnelle permet des calculs plus rapides et plus puissants.

Elle a par contre un inconvénient : la position peut être ambigüe.

Les zéros et leurs inventions

Les inventions du signe zéro ont été faites au moins trois fois et indépendamment : à Babylone entre 400 et 700 ans avant JC, par les Mayas dans les premiers siècles de notre ère et par les Indiens vers le 4ème siècle. Mais ces inventions couvrent des notions différentes : zéro comme marque d'un espace vide, zéro comme chiffre qui peut jouer le rôle de multiplicateur, et zéro comme nombre ou valeur.
Le zéro moderne correspond à la version indienne, qui s'est diffusée dans le monde arabe avec Al Khwarizmi, puis en Europe et dans le monde entier à la Renaissance avec Leonard de Pise.

• Le zéro a d'abord été une solution pour marquer une place vide, au milieu d'un nombre.
  Il lève l'ambiguité sur la position (donc la valeur) des chiffres dans la numération positionnelle.
  • Il est donc nécessaire chez les Sumériens pour lever l'ambiguité quand un des chiffres ou une puissance de 60, est nul. Les Babyloniens (~700 ans avant notre ère), ont utilisé un signe, 2 ou 3 clous inclinés, pour marquer cette place vide. Par exemple :
    peut valoir 375 (6x60 + 15) ou 21615 (6x3600 + 15),
    deux clous inclinés permettent de lever le doute,
    mais cette arrivée du zéro attendra plus de 1000 ans.
  • Cette même notion de zéro est inutile chez les Romains dont les symboles sont différents pour les unités, les dizaines, les centaines et les milliers : 3615 s'écrit MMMDCXV, et 3015 s'écrit MMMXV sans avoir besoin d'un zéro.
• Le zéro en tant que chiffre (qui peut être à droite d'un nombre), n'apparait que plus tard, vers 300 ans avant notre ère. Il permet de préciser la valeur absolue d'un nombre, en passant des unités aux dizaines, aux centaines, etc.
  Son fonctionnement est décrit en 1430 dans le compendi de l'art de l'algorisme, déjà cité :

  Le dixième signe « 0 » est appelé zéro et ne vaut rien en lui-même 
  mais permet de changer la signification des autres signes de la façon suivante :
  	« 1 » vaut pour une unité
  	« 10 » vaut pour une dizaine, ou dix unités
  	« 20 » vaut pour deux dizaines, ou vingt unités
  	et ainsi de suite jusqu’à « 90 » qui vaut pour neuf dizaines, ou quatre-vingt-dix unités
  	« 100 » vaut pour une centaine, c’est à dire dix dizaines
  	« 200 » vaut pour deux centaines, ou vingt dizaines
  	et ainsi de suite jusqu’à « 900 » qui vaut pour neuf centaines
  
  Rajouter un zéro à droite change ainsi la signification du signe en compte soit d’unités, 
  soit de dizaines, soit de centaines, et ainsi de suite, de façon qu’un zéro de plus à droite 
  donne une valeur dix fois plus grande.
  

  Jusque là, les nombres sumériens utilisés pour calculer sont 'flottants':

  peut valoir 3600, 60, 1, 1/60, ...

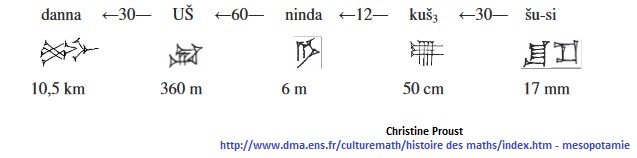
  mais ça n'est pas vraiment gênant, dans la mesure où à la fin des calculs, le résultat est converti en unités 'concrètes' ou le zéro n'est pas utile. Les Sumériens avaient leurs tablettes de conversion, par exemple pour les unités de longueur :
  Supposons par exemple, que le calcul de la largeur d'un champ donne ou 2:30.
  On peut l'interpréter comme 150 su-si (2,55m) ou 60 fois plus (153m), ou 3600 fois plus (9km), mais il ne fait pas de doute pour le scribe que la bonne réponse est 150 x 60 su-si soit 25 ninda(153m). Les autres valeurs n'ont pas de sens dans ce contexte.
  
  
• Le zéro en tant que nombre.
  Zéro peut être un nombre ou une valeur, le résultat d'une mesure ou d'un calcul. Il apparait chez Ptolémée vers l'année 150.
  Il permet d'expliciter une valeur nulle, de la distinguer d'une case vide ou non renseignée.

Il faudra attendre 1202 et le liber abaci, de Léonard de Pise (alias Fibonacci), pour que l'invention du zéro commence à se diffuser dans le monde chrétien.

Remarquons que le zéro a été inventé à des périodes et dans des régions différentes.
C'est aussi le cas de la base 10 utilisée dans de nombreuses contrées, en Chine avec des baguettes qui remplacent les pierres, et chez les Incas avec les quipus et les yupanas, … et l'inventaire des historiens se limite aux cultures qui ont laissé des traces que l'on a retrouvées et interprétées.