La multiplication la plus rapide de tous les temps, et sans erreur.

Le besoin de tables numériques

Les Sumériens ont utilisé les tables numériques pour l'enseignement. Des milliers de tablettes ont été retrouvées, en particulier à Nippur. Ce sont des tables de multiplication, des carrés et d'inverses (en sexagésimal) et des correspondances entre les différents systèmes utilisés pour mesurer les longueurs, sufaces, volumes, poids,... et le système sexagesimal qui était utilisé pour les calculs.

Avec le développement de la banque, des assurances et de la comptabilité des entreprises, explose le besoin en tables fiables facilitant les calculs, les multiplications, les pourcentages, l'actualisation... Avec la navigation, les tables trigonométriques permettant de faire les calculs de longitude et latitudes deviennent des outils indispensables. Et quand Neper invente les logarithmes, la nécessité des tables numériques s'impose comme une priorité.

Le défi de la construction de tables importantes, précises et fiables devient un sujet pour les mathématiciens du 19ème siècle. En 1821 Charles Babbage présente sa "machine à différences" qui vise à calculer automatiquement toute fonction qui peut être approximée par des polynômes. En France, la première édition des tables de logarithmes de Bouvart et Ratinet est parue autour de 1900, elle sera utilisée par des générations d'ingénieurs en complément de la règle à calcul jusqu'à l'apparition des calculatrices électroniques au milieu des années 1970. La table Laborde comporte ainsi sur près de 200 pages les puissances des nombres de 0 à 1000, les racines, les exponentielles, les logarithmes et les fonctions trigonométriques et hyperboliques. Et tout cela calculé au 19ème siècle et au début du 20ème, donc sans ordinateur ...

Multiplier avec la table de logarithmes

Petit rappel (ou plus) sur la multiplication avec les logarithmes qui s'appuie sur la relation
Log(ab) = Log(a) + Log(b).

Soit à multiplier 365 par 76

1. Lire dans la table le logarithme de 365 : 5.899897
2. Lire dans la table le logarithme de 76 : 4.330733
3. Additionner les deux logarithmes : 10.230630
4. Lire dans la table à quel chiffre correspond ce logarithme : 27 739.98

Pour un résultat exact à 27 740, la précision est excellente ! Avec cette méthode nous avons remplacé une multiplication par 3 lectures dans une table et une addition. Et ceci quels que soient les nombres multipliés (dans la limite de la capacité de la table) et avec la fiabilité et la précision apportées par la table.

On comprend que ces tables aient satisfait les besoins des ingénieurs jusqu'en 1970.

Utiliser une table des carrés pour multiplier

L'inconvénient des tables de logarithmes est que le résultat ne peut être qu'une approximation, certes excellente, mais insuffisante pour les besoins des comptables qui ont un souci au cent près.

Deux solutions à cela : des tables de multiplication très épaisses, comme la table Le Pelletier, cf infra, ou le recours à une astuce qui n'utilise que les tables des carrés. Elle utilise l'identité remarquable :
(a+b)² - (a-b)² = 4 a b

Soit à nouveau à multiplier 365 par 76

1. Calculer 365 + 76 = 441
2. Lire dans la table son carré : 194 481
3. Calculer 365 - 76 = 289
4. Lire dans la table son carré : 83 521
5. Oter ce second carré du premier : 110 960
6. Diviser par 4 : 27 740

Le résultat est exact. On a remplacé une multiplication par 2 additions, 2 lectures dans une table, et une division triviale par 4 (ou, si on a des affinités égyptiennes, deux divisions par 2).

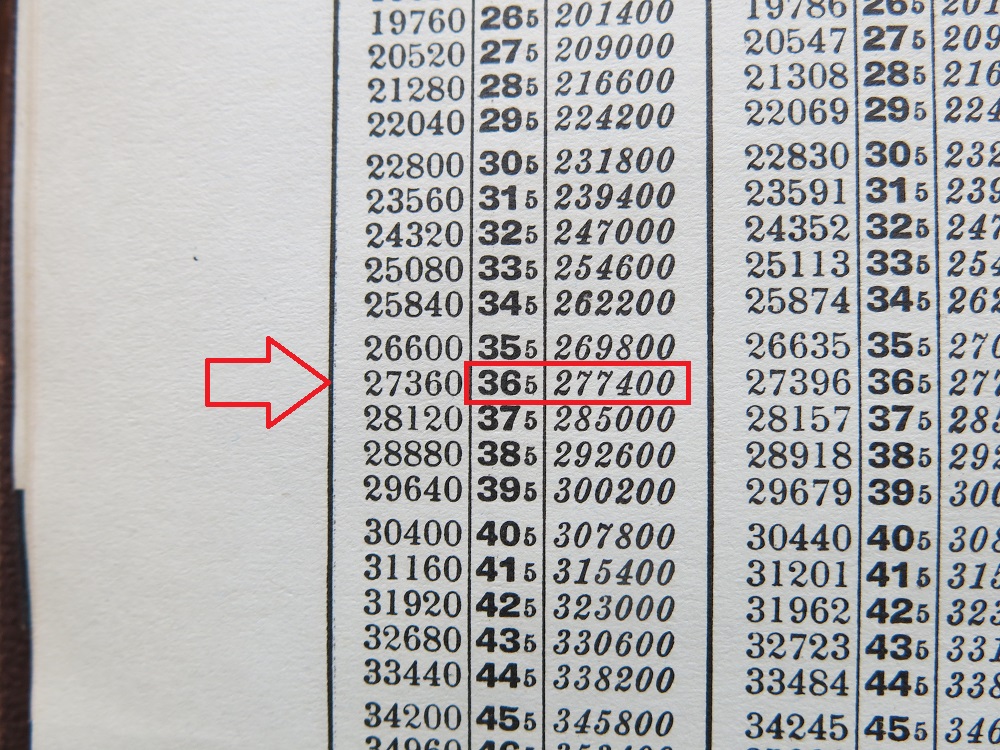
Un exemple pour les commerçants : le calculateur Le Pelletier

Le calculateur utilisé pour la vidéo ci-dessus date de 1931. Il donne in extenso sur plus de 200 pages toutes les multiplications de nombres à 3 chiffres (de 0 à 999) par des nombres à 2 chiffres (de 0 à 99) et à 3 chiffres terminant par 5 (exemples 105, 235, 995,...). Il donne également l'inverse de tous les nombres à 3 chiffres ainsi que des calculs d'intérêts et la division par 12 pour la mensualisation.

La multiplication de 365 par 76 est en lecture directe dans ces tables. Si on parle de temps passé ou de risque d'erreur, c'est imbattable ! Mais bien sûr, dans les limites des capacités de cette table numérique préconstituée.

Dans un premier temps, on choisit la page recherchée, ici la table de 76.	Et dans un second temps, on lit directement le résultat en face de 365 : 27 740.