Les bâtons de Neper
Neper et le calcul
En 1617, quelques mois avant sa mort, Neper publie un ouvrage "Rabdologiae", où il présente trois outils pour faciliter les calculs.
- les bâtons pour multiplier (sans connaître ses tables),
- une table à jetons pour multiplier en binaire,
- le promptuario.
Neper
|
Neper est l'inventeur des logarithmes 'néperiens' que l'on apprend au lycée.
Le logartithme est une fonction qui tranforme une multiplication en addition : Log(a x b) = Log(a) + Log(b)
Neper a voulu simplifier le calcul avec cette fonction, et s'est rapidement rendu compte qu'il fallait disposer de "tables" pour ces logarithmes. Pour établir ces tables il faut faire une énorme quantité d'opérations. La vitesse et la fiabilité des opérations de base doivent donc être améliorées. |
|
Les bâtons de Neper :
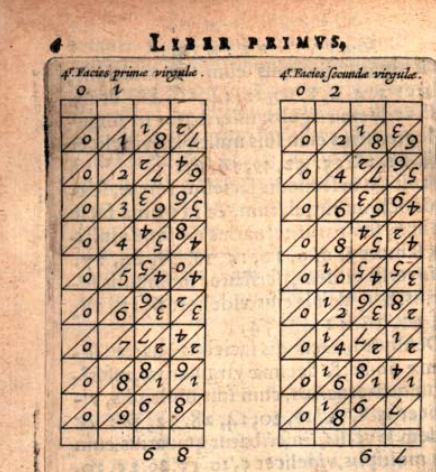
Ils permettenr de multiplier sans connaître les tables de pythagore. On dit aussi Napier's rods ou Napier's bones en anglais. "Neper" est la signature qu'utilisait John Napier, baron de Merchiston, quand il écrivait en latin.
(Voir la description des bâtons sur wikipedia )
La table à jetons pour multiplier en binaire :
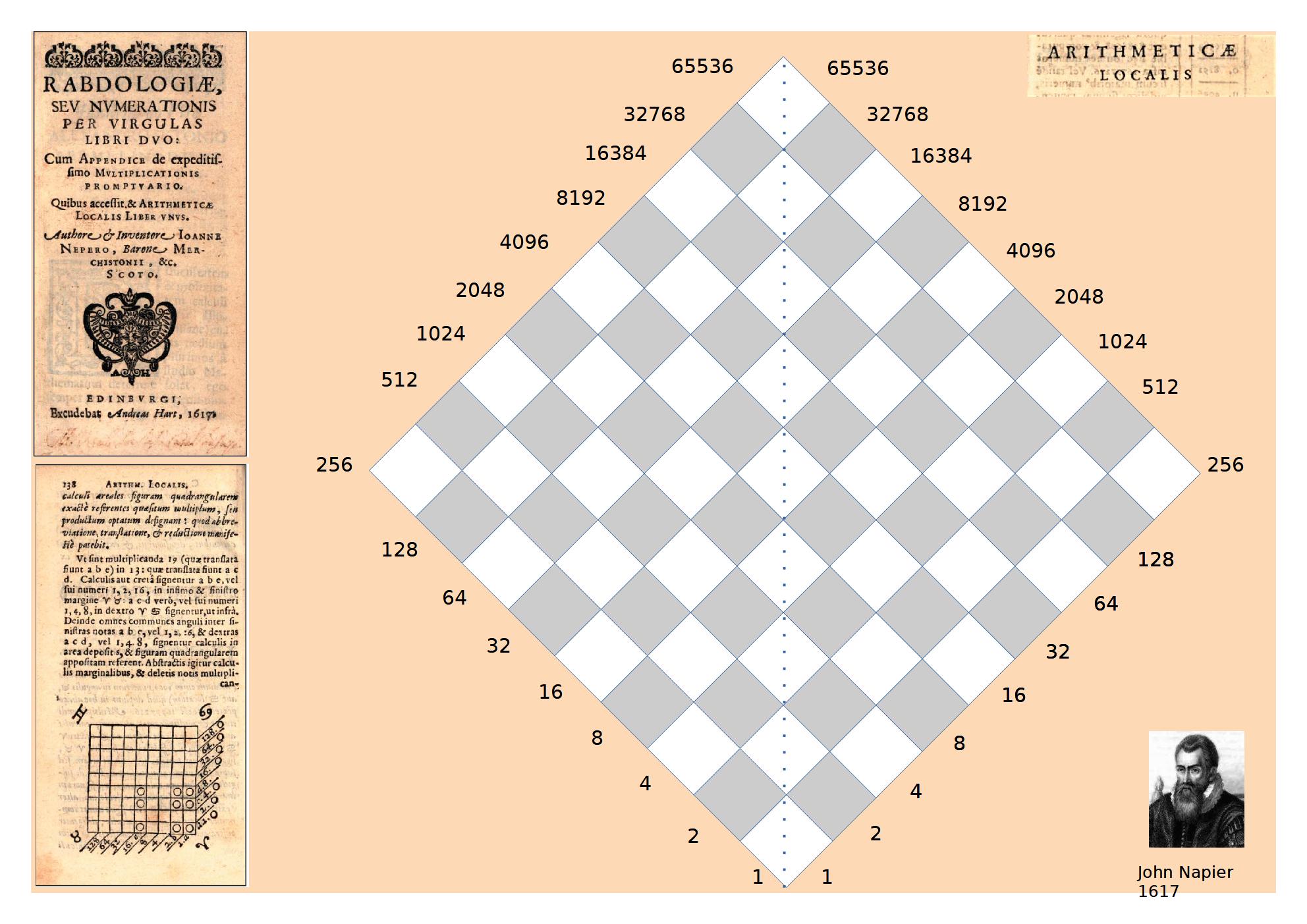Le deuxième outil, plus exploratoire, est une table à jetons permettant de faire des multiplications en binaire. Vous pouvez en télécharger notre reconstruction ici. La démarche reprend le principe de la multiplication égyptienne : une fois que les multiplicandes et multiplicateurs sont décomposés en somme de puissances de 2, la multiplication devient triviale.
La vidéo suivante en présente le fonctionnement.
Le promptuario :
Le troisième outil est un prolongement des bâtons de Neper. Ceux-ci sont limités à des multiplicateurs à un seul chiffre, et il faut reporter à la main les additions à faire, avec le risque de se tromper dans les décalages. Le "promptuario multiplicandis" a l'ambition de résoudre ces problèmes en permettant la multiplication par des nombres à plusieurs chiffres.
Il existe un exemplaire de cet instrument datant probablement de la fin du 17ème ou du 18ème siècle dans un musée espagnol, le (Museo Arqueologico Nacional ). L'exemplaire sur la photo est une réalisation pour le site www.aventureducalcul.fr par Artisabois 93.
Sur les bâtons verticaux, on porte le multiplicande et sur les horizontaux le multiplicateur. A chaque intersection apparait le résultat de la multiplication partielle d'un chiffre du multiplicande par un chiffre du multiplicateur, dans la même disposition que dans la multiplication "per gelosia". Il ne reste donc plus qu'à sommer selon les diagonales pour avoir le résultat.