Les animaux calculent, les Mésopotamiens ont posé la base de la numération, et ensuite ?

Dans de nombreuses langues, la façon de dire les nombres est à la fois additive et multiplicative. Prenons l'expression : trois cent soixante cinq.
Si on écoute bien, on entend trois fois cent plus six fois dix (la terminaison en "ante") plus cinq unités.
On transcrit ensuite en "mathématique" : 3 x 100 + 6 x 10 + 5 ,
et grâce à la numération positionnelle inventée par les Sumériens on écrit 365 en base 10.

Prenons l'expression : trente mille quarante. On entend bien trente fois mille et quatre fois dix. On ne dit pas le zéro centaines ni le zéro unités. Ils sont inutiles à l'oral. Et on écrit 30 040.

Et maintenant comment passer de cette base à la maîtrise des 4 opérations, addition, soustraction, multiplication, division, avec quelques incursions vers l'élévation au carré et son inverse, l'extraction de racine carrée ?

L'addition

Additionner, c'est prendre 2 paquets de billes et, sachant combien de billes il y a dans chaque, dire combien il y en aura en les mettant toutes dans un même paquet.

L'addition est très proche de notre façon de dire les nombres, comme dans l'exemple ci-dessus avec 365. Elle apparaît donc assez naturelle, mais néanmoins :

• Il faut apprendre les tables élémentaires (pour nous de 1+1 = 2 à 9+9 = 18),
• puis acquérir la maîtrise de la retenue (1+9= 10, 1+999= 1000,...),
• et surtout vérifier qu'on n'ajoute que des objets de même type (des chous et des carottes, ça peut faire une soupe mais pas une addition).

Si vous pensez que c'est trivial, et qu'il n'y a pas lieu à développements, allez voir le champion du monde de Flash Anzan.

La soustraction

La soustraction peut être vue comme l'inversion de l'addition. Au lieu de rajouter des billes dans un paquet, on en enlève et on veut savoir combien il en reste.

La gymnastique calculatoire est un peu plus complexe que l'addition. Nous aurons l'occasion de voir comment cela complique le calcul mécanique, et en particulier celui de la retenue. (nb : le problème d'enlever 10 billes à un sac qui n'en contient que 5 ne sera pas traité ici, voir l'invention des nombres négatifs.)

La multiplication : conduire l'enquête

La multiplication est beaucoup plus complexe que l'addition. D'abord, quand on additionne on a des billes au départ et on a toujours des billes à la fin. On ne peut additionner que des choses semblables.

Pour la multiplication on a, potentiellement, trois types différents. On peut multiplier une surface par une longueur et le résultat sera un volume.
La multiplication n'est pas une addition répétée.
Ajouter des surfaces n'en fera jamais un volume !
Et, par ailleurs, si on multiplie par 0,5 , que pourrait vouloir dire qu'on additionne 0,5 fois ?

Dans la suite nous allons voir comment multiplier et parfois diviser à la manière des Egyptiens, des Romains, au moyen âge avec des jetons ou à la plume, ou avec des machines. A chaque fois c'est différent !

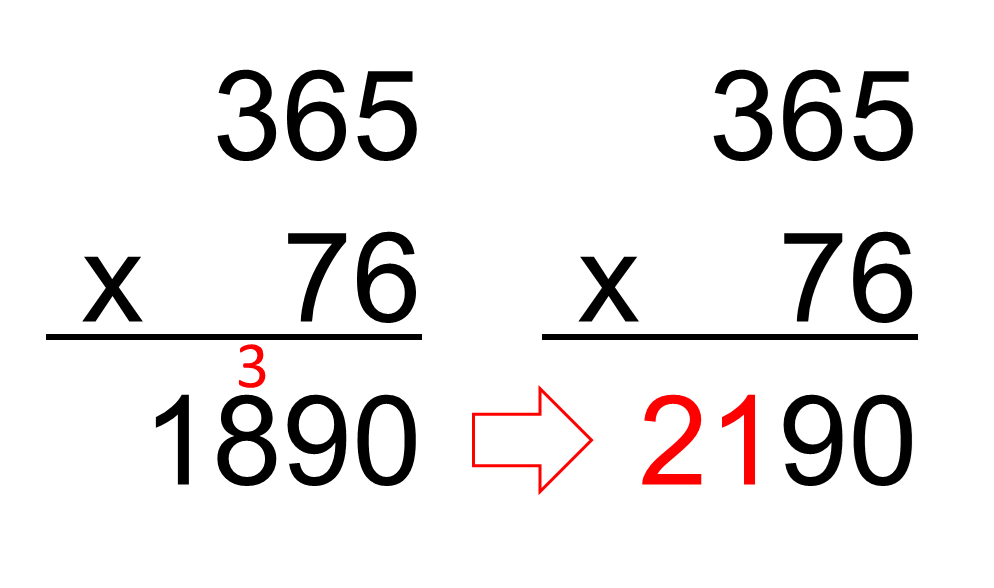
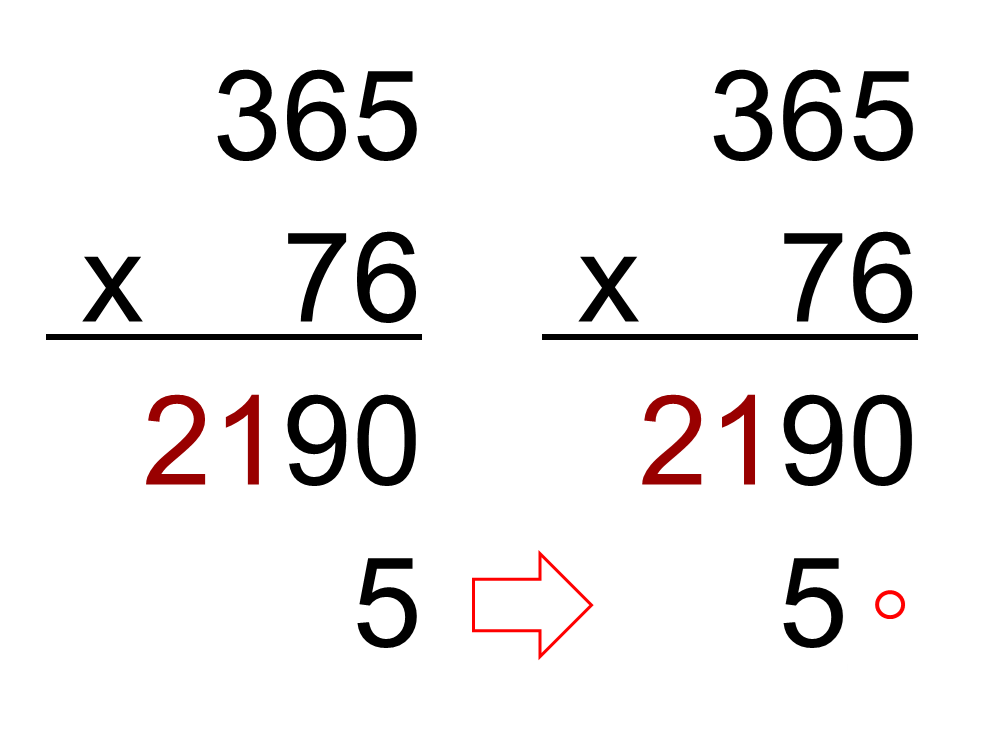
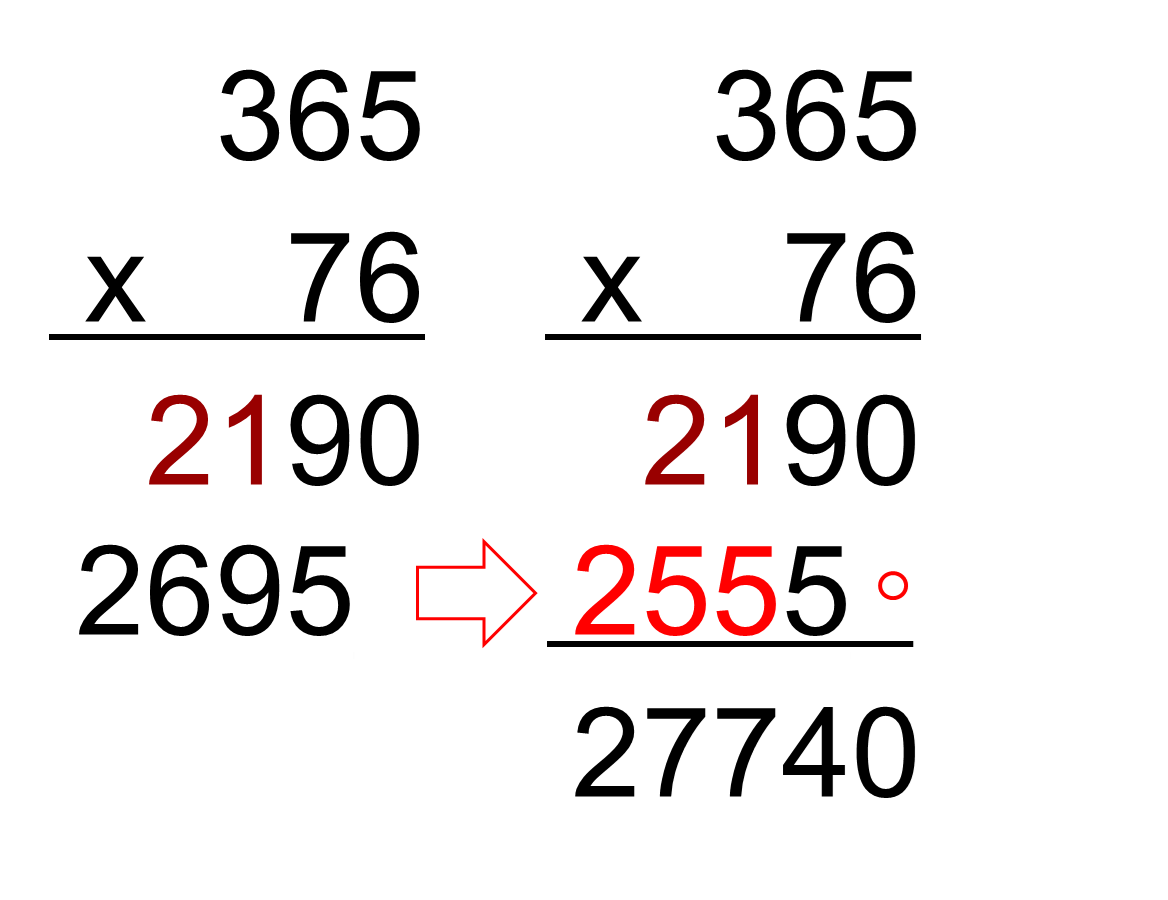
Le calculateur prodige de la vidéo a fait, dans l'ordre, ces 3 erreurs :

de retenue : 6 fois 6, 36 la retenue 3 doit être ajoutée à 6 fois 3 18 pour écrire 21, de procédure en oubliant de décaler la ligne quand on multiplie par 7 dizaines, de table de multiplication : 7 fois 6 ne font pas 56 mais 42.

Et le résultat final correct est bien sûr 365 x 76 = 27740.
Comme le souligne Stella Baruk, l'analyse des erreurs permet ainsi de comprendre le cheminement erroné et de revenir vers les étapes à corriger.

Multiplier les multiplications

Cet exemple montre que notre méthode habituelle n'est ni la seule ni, dans certains cas, la meilleure. On déroule dans cette vidéo la multiplication de gauche à droite, en commençant par les chiffres qui portent les centaines puis les dizaines. On va prendre en compte les années bisextiles, avec un jour de plus tous les 4 ans, ce qui correspond à une année moyenne de 365,25 jours à multiplier par 76.
Déroulez cette multiplication et vous devriez trouver 27759,00 à la fin.

La multiplication des 2 nombres consiste à multiplier chacun des chiffres du premier nombre par chacun des chiffres du second, en tenant compte de leur position (unité, dizaine ou centaine) et à ajouter ces produits. On peut le faire dans l'ordre qu'on veut, par la droite dans la méthode habituelle et en partant de la gauche ici.

Le principal intérêt de cette méthode est de commencer par les chiffres les plus importants, ce qui permet d'avoir rapidement une bonne estimation du résultat. A la moitié du calcul, après 5 multiplications, le cumul est de 27 710, à 2 millième du résultat final et après 7 multiplications, à 2 10 000ème près !
Par comparaison, avec la méthode habituelle on n'a pas la moindre idée du résultat final après la 7° multiplication. La 2° méthode est ainsi beaucoup plus rapide pour avoir une idée approchée du résultat, par exemple pour faire ses courses. La précision de 0,2% suffit souvent et on peut s’arrêter après la 5° multiplication.

Cet exemple montre que différentes méthodes existent et que chacun peut choisir sa manière de multiplier selon son objectif. Si vous êtes commerçant et pressé, la 2° méthode va vous convenir, et c’est plutôt comme ça que nos ordinateurs calculent, ça va plus vite.

La division

La soustraction peut être envisagée comme l'inversion de l'addition, et de même la division comme l'inversion de la multiplication.

Mais il y a deux différences importantes entre la multiplication et la division qui font de cette dernière un calcul beaucoup plus délicat.

Premièrement vous pouvez toujours multiplier deux nombres pris au hasard, quelle que soit la notation que vous adoptez.
Il n'en va pas de même avec la division.
Si vous divisez 10 par 3 en notation décimale vous aurez 3.33333333... qui ne se terminera jamais. C'est bancal et vous pouvez :

• Soit dire 10/3 = 3 et il reste 1, et la division au lieu de vous donner un résultat vous en donne deux : le quotient et le reste.
• Une deuxième solution serait de ne diviser que des nombres divisibles, c'est à dire des nombres pour lesquels il est possible d'obtenir un quotient avec un nombre fini de décimales, sans reste. Cette deuxième solution a été adoptée par les Mésopotamiens.
• Une troisième solution serait d'admettre 10/3, ou 1+ 1/3, comme une nouvelle notation de nombres possibles (cette troisième solution a été adoptée par les Egyptiens), et vous aurez inventé les nombres rationnels.

Deuxièmement, la multiplication est commutative et distributive par rapport à l'addition :
(a+b+c)x d = ad+bd+cd ce qui permet de procéder par multiplications partielles et cumul et dans n'importe quel ordre car : (a+b+c)x d = ad+bd+cd = dc+db+da.

La division qui n'a pas cette propriété bénie sera donc plus complexe. Ceci explique pourquoi il a fallu attendre le 18ème siècle pour que les méthodes pour la division soient définitivement établies.

Les carrés et racines carrées

Elever un nombre au carré, c'est le multiplier par lui même. Sous l'angle du calcul, il n'y a pas de grande différence entre cette élévation et la multiplication. Toutefois, les carrés jouent des rôles importants en géométrie (Pythagore) et les apprentissages arithmétiques incluaient, dès l'antiquité, leur maîtrise.

Extraire une racine carrée, c'est plus compliqué, et ce sera en quelque sorte le sommet de l'arithmétique que nous considèrerons dans ce site. Sommet déjà attaqué par les Mésopotamiens comme on l'a vu avec la tablette YBC 7289.