Nous sommes tous des calculateurs mentaux

On calcule avant d'écrire. Chacun d'entre nous dans nos apprentissages, comme les humains l'ont fait il y a 5000 ans (voir les commencements). Et chacun est à un niveau différent de maîtrise de ces calculs et peut progresser à partir de ce niveau.

On commence par +1 , et on ne s'arrête plus

Le premier calcul se fait par la numération : 1, 2, 3, 4 et la vision de cette progression comme une addition de +1 répétée.
Ensuite, on étend progressivement : + 2, + 3,...
Et on apprivoise la table d'addition de 1 + 1 = 2 à 9 + 9 = 18
Et là se présente une bifurcation :

Si la seconde voie vous tente, voilà tout d'abord un outil pour voir où vous en êtes. Vous connaissez bien vos tables d'addition et de multiplication :

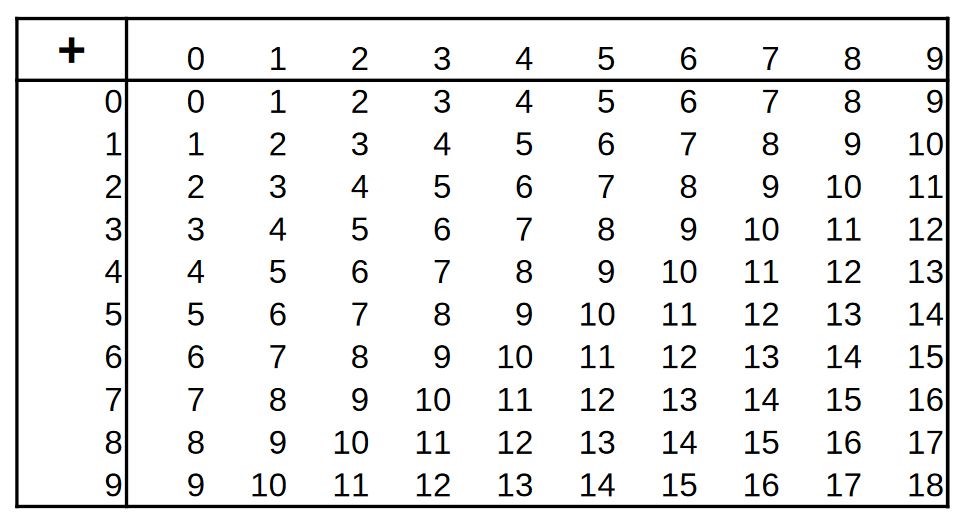
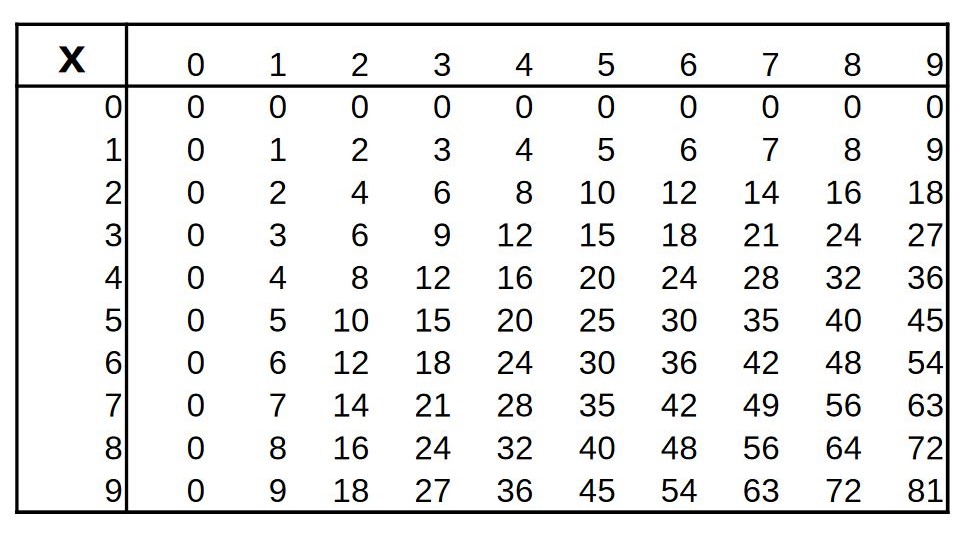
Maintenant, remplissez le plus vite possible les deux tables suivantes, où lignes et colonnes ont été mélangées (vous avez un pdf ici ) :

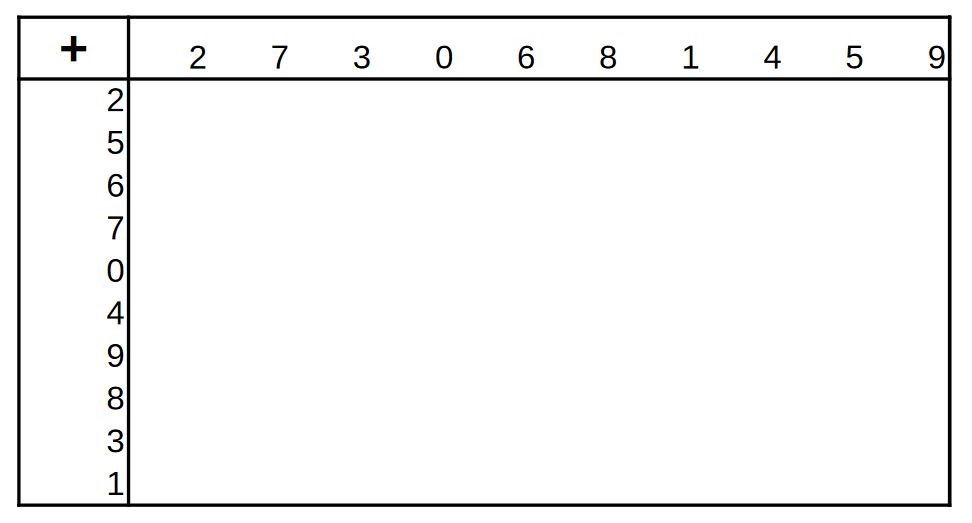
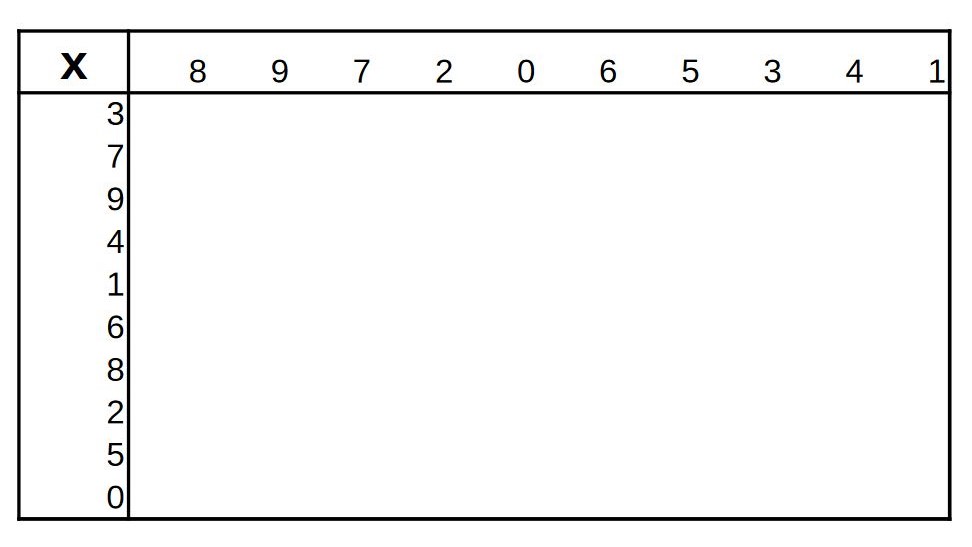
Après ce test, vous savez où vous en êtes pour ce premier niveau d'arithmétique. Test que vous pouvez prolonger en remplaçant addition et multiplication par soustraction et division.

Observez là où vous avez écrit le résultat juste immédiatement, là où il vous a fallu réflechir et recalculer, et peut-être, quelques erreurs ?
Les différents trucs proposés ci-après ont tous le même objectif : progresser dans la maîtrise de ces tables d'additions et de multiplications de nombres à, au moins, 2 chiffres... et plus si affinités.

Ces trucs sont utiles pour l'apprentissage et pour lever le doute, mais bien sûr ils deviennent progressivement moins utiles quand, les ayant pratiqués, est venue la maîtrise automatique spontanée du calcul.

Additionner

Se rapprocher des bords : puisqu'on commence par +1, autant s'appuyer sur ce qu'on connait le mieux :
+ 2 c'est +1 +1
+ 3 c'est +1 +2 ou +2 +1 ou +1 +1 +1
+ 9 c'est +10 -1, c'est-à-dire, augmenter de 1 les dizaines et diminuer de 1 les unités.

Ajouter 10 , c'est ajouter 1 à la dizaine, on reste sur les bords ...

Et plus largement, se rapprocher du plus facile, quelques exemples :
ajouter 97 c'est ajouter 100 puis enlever 3
ajouter 18 c'est ajouter 20 puis enlever 2, c'est aussi ajouter 9 puis 9 : à chacun son truc !

Les comptes qui s'entendent

Notre numération est additive, de nombreuses additions s'entendent si on les écoute :
20 + 5 = vingt et cinq
300 + 9 = trois cents neuf
Et l'oreille peut s'aiguiser : "ante" , ça multiplie par 10 (quarante, cinquante,...)
Mais il y a des vilains canards :

Les comptes qui se voient

Regardez votre main, doigts dépliés, 5 doigts.
Repliez un doigt, vous voyez un doigt plié et quatre dépliés, donc vous voyez 1+4 =5
Avec les deux mains, vous voyez de la même façon que 3+7 = 10 et 4+6=10

Pour visualiser l'addition, utilisons la ligne numérique. Une bande de papier, des graduations, et vous voyez comment ajouter 4 fait avancer de 4 cases le repère sur la ligne. Et la soustraction vous est offerte en prime par Stanislas Dehaene !

Multiplier

Pour multiplier, doubler d'abord

Le doublement est la première des multiplications, la maîtriser à l'endroit et à l'envers est mentionné dans tous les traités du moyen âge comme un premier pas vers les autres multiplications.

On peut ensuite facilement multiplier par 4 (ou 8) : c'est multiplier 2 fois (ou 3) par 2

En combinant cela, pour multiplier 365 par 76 on peut faire les étapes suivantes :
On constate que 76 = 80 - 4
Le doublement répété de 365 donne 730 1460 2920
Donc 365 x 76 = 29200 - 1460 = 27740

Autre exemple, soit à multiplier 28 par 15. On constate que 28 = 4 x 7, et que 15 x 4 = 60,
on a donc 28 x 15 = 7 x 60 = 420.

Multiplier par 10

La numération décimale positionnelle rend particulièrement immédiate la multiplication par 10 : il suffit de rajouter un zéro à droite. Et, comme le dit Leibniz dès le 17ème siècle, ce sont toutes les multiplications qui sont aussi triviales si on adopte le système binaire !

Et on peut ensuite multiplier par 9 : c'est multiplier par 10 et enlever 1

Etre au carré

Dans toutes les méthodes depuis l'antiquité, une place à part est faite aux carrés. Des tables des carrés des n premiers entiers existent depuis 5000 ans à Sumer.

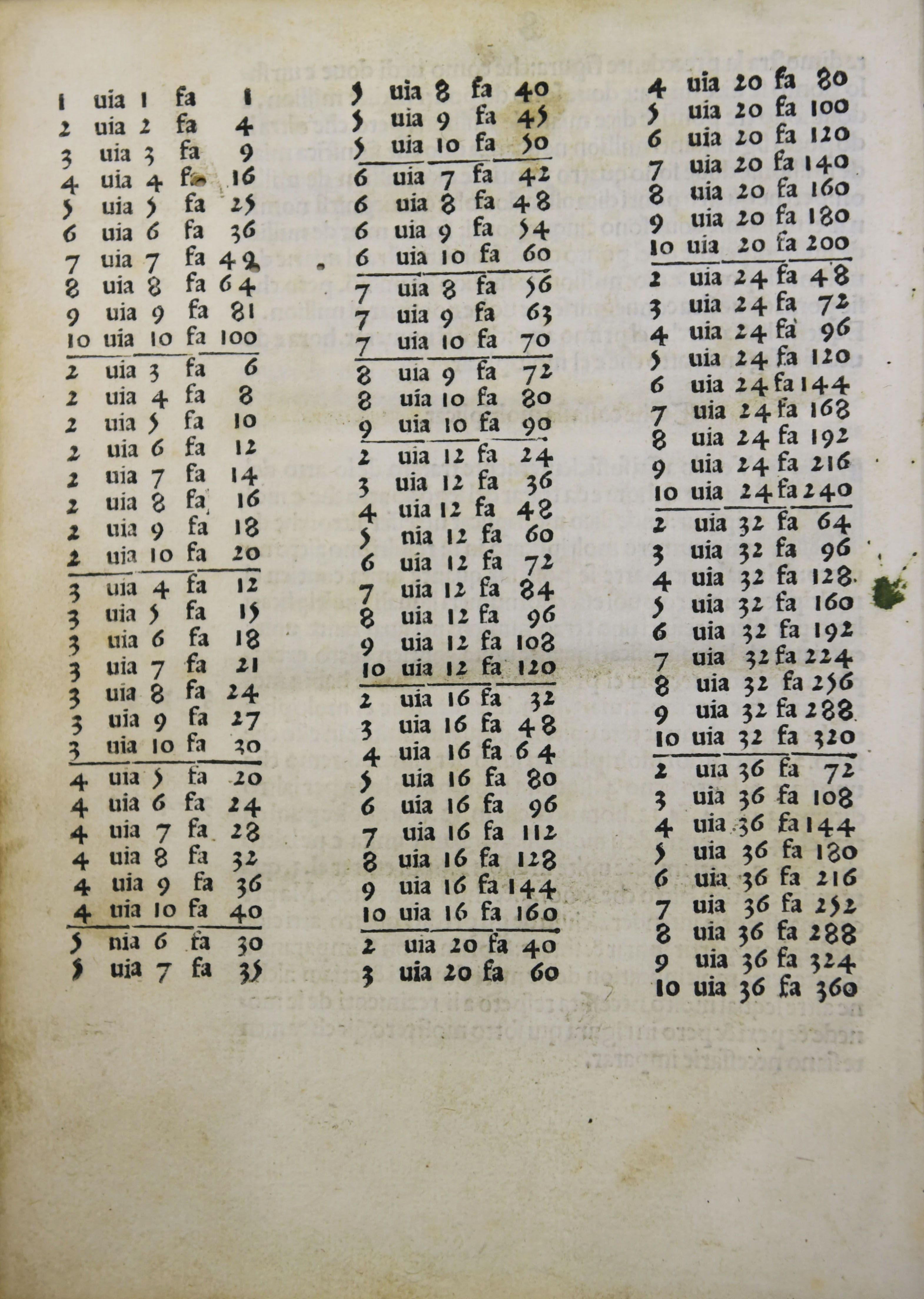Cette table est issue du Libro de abacho de Pietro Borghi imprimé à Venise le 10 décembre 1501, (bibliothèque universitaire de Lyon) ce qui en fait un des premiers ouvrages d'arithmétique commerciale imprimés. Dans cette table, l'auteur commence par donner tous les carrés de 1 à 9, puis les tables de 2, 3, jusqu'à 9 puis les tables de 12 16 20,... mais, contrairement à ce que nous faisons, en économisant la symétrie.

Certains carrés sont très faciles à calculer. Par exemple, les nombres se terminant par 5, de la forme n5 ont un carré de la forme n(n+1)25. Ainsi le carré de 35 est 1225 car 3 x 4 = 12

N'utiliser que les multiplications par 2 5 10

Soit à multipier 365 x 76
Je calcule d'abord 365 x 2 = 730
puis 365 x 5 = 1825 (c'est aussi multiplier par 10 et diviser par 2)
Ensuite je regarde 76 , c'est 50 + 20 + 5 + 1 , décomposition (triviale) en somme avec des 1, 2 , 5 unités, dizaines,..
Vient immédiatement : 365 x 76 = 18250 + 7300 + 1825 + 365 = 27 740

La règle des paresseux

L'apprentissage des tables de multiplication est un passage obligé vers l'arithmétique telle que nous la pratiquons.
On peut se simplifier la tâche en n'apprenant que les tables jusqu'à 5 et en retrouvant les suivantes avec la règle des paresseux : la Regula Pigri.

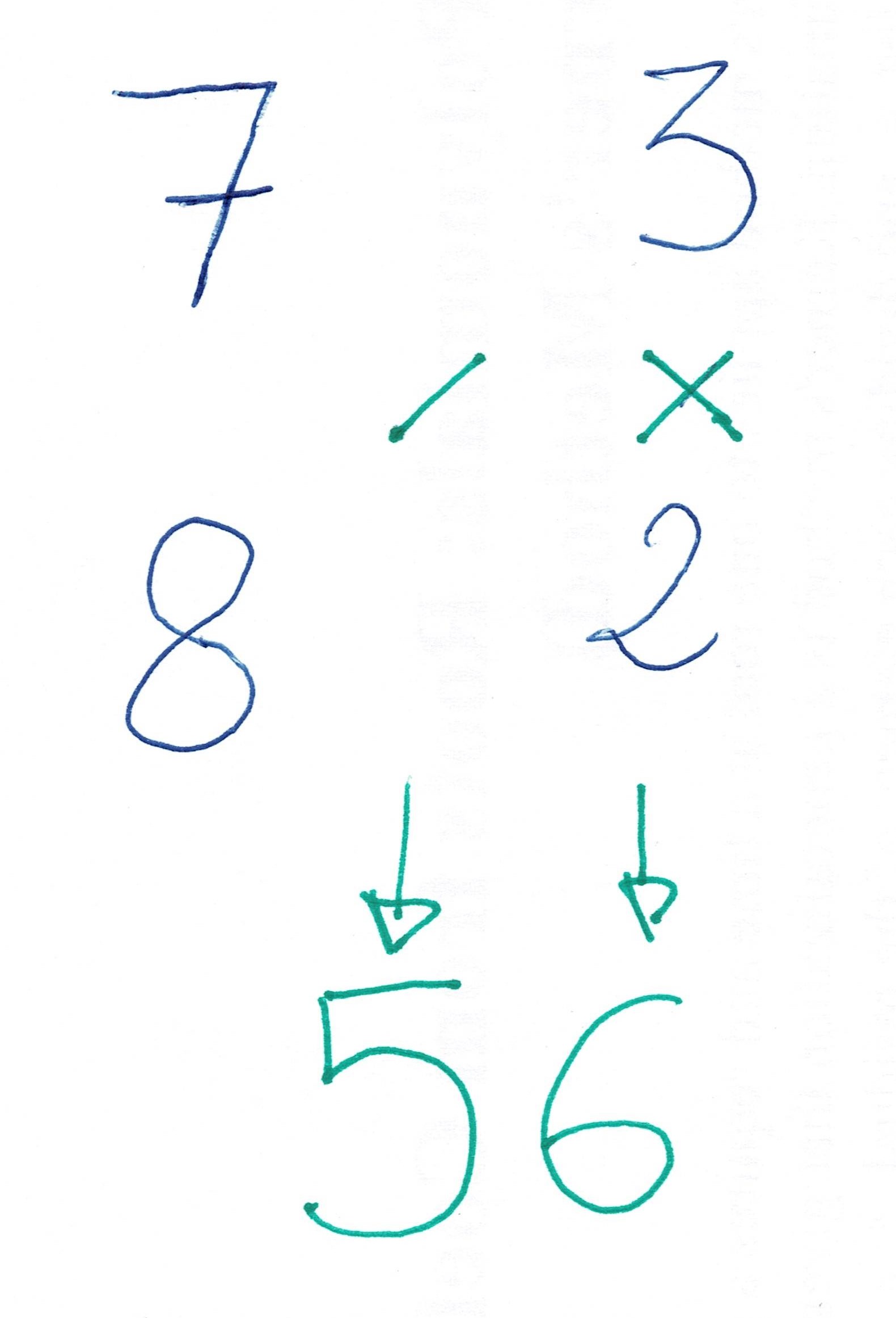Soit à retrouver 7 x 8
On prend les compléments à 10, donc 3 et 2.
Le produit des compléments 3x2 est 6, on a les unités.
La différence en diagonale 7-2 = 8-3 = 5 , on a les dizaines.
Le résultat est donc 7 x 8 = 56 !

Si la soustraction en diagonale vous déplait, vous pouvez ajouter les 2 nombres à multiplier (ici 7 + 8 = 15) et enlever 10, vous obtenez 5 , le nombre des dizaines recherchées.

On a aussi dans la vidéo ci-dessous une variante de cette méthode avec les doigts :

La mentalisation du boulier

Les trucs présentés plus haut s'appuient sur le calcul "à la plume" qu'il s'agit de faciliter en mémorisant le plus possible de résultats élémentaires et en développant des stratégies pour les assembler.

Il y a d'autres approches totalement différentes. Par exemple, pour les utilisateurs de bouliers on peut, avec un entraînement substantiel, mentaliser le boulier, c'est à dire le voir et le manipuler dans sa tête sans plus avoir besoin du support matériel. Et les résultats sont étonnants.