Pile ou Face, Expérimentation
Durée estimée: 45 minutes
Présentation
|
Pile ou Face : l'expérimentation.
Dans cette leçon, vous allez utiliser une application déjà faite, pour conduire une expérience dont l'objectif est de déterminer si les blocs de App Inventor sont de bonne qualité pour générer des nombres aléatoires.
L'application vous permet d'effectuer N tirages au sort avec une pièce, d'afficher les résultats et de calculer le pourcentage moyen du côté face. Ce que l'on attend, c'est que lorsque N augmente, la moyenne se rapproche de 50%.
Objectifs: Dans cette leçon vous allez :
|
Contexte
Voici quelques informations que vous devez connaitre sur la manière dont les ordinateurs et les langages informatiques (comme App Inventor) génèrent des nombres aléatoires :
- Les nombres aléatoires sont utilisés dans un grand nombre de programmes, en particulier dans les jeux (comme Android Mash) et les simulateurs (comme PileOuFace).
- Il est difficile de créer un processus qui soit purement aléatoire. Pourtant les processus aléatoires sont couramment utilisés par les ordinateurs.
- Puisque la création d'un processus purement aléatoire est difficile, les programmes utilisent ce que l' on appelle des générateurs de nombres pseudo-aléatoires (abrégés PRNGs en anglais pour : Pseudo Random Number Generators). C'est bien plus facile que de générer des nombres vraiment (complètement) aléatoires. Si la manière dont fonctionnent ces générateurs (PRNG) vous intéresse, la leçon suivante va rentrer dans le détail.
- Les PRNGs (générateurs de nombres pseudo aléatoires) génèrent une série de nombres qui "semblent aléatoires".
- Les PRNGs sont des modèles de générateurs de nombres purement aléatoires. Comme tels, ils peuvent être 'bons' ou 'mauvais' selon la précision avec laquelle ils s'approchent d'un mécanisme purement aléatoire. Les PRNG sont des sujets importants de recherche en mathématique et en informatique.
- App Inventor utilise un générateur standard et reconnu qui doit répondre nos besoins.
L' Expérience
Notre application PileOuFace simule le tirage au sort avec une pièce. Si vous tirez au sort avec une pièce (équilibrée) un très très grand nombre de fois (par exemple un million de fois), alors la moyenne des piles et des faces devrait être très proche de 50%. D'où l'expression d'un tirage à 50:50.
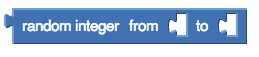
Le bloc App Inventor entier aléatoire entre _ et _ utilise un PRNG pour générer une séquence d'entiers. Dans notre application c'est entre 1 et 2, les bornes étant comprises. Donc si le PRNG est de bonne qualité, il devrait générer des 1 dans la moitié des cas et des 2 dans l'autre moitié.
Donc ça devrait être un bon modèle de notre tirage à pile ou face.
Hypothèse
L'hypothèse que nous allons évaluer est que le bloc générateur de nombres pseudo-aléatoires (PRNG) utilisé par App Inventor est de bonne qualité, c'est à dire qu'il fournit une bonne approximation d'un processus qui génère des 1 et des 2 de façon purement aléatoire.
Si vous vouliez vérifier qu'une pièce de monnaie n'est pas biaisée (ou bien équilibrée) pour tirer au sort, vous feriez de nombreux tirages à pile ou face en comptant le nombre de côtés pile et le nombre de côté face. Pour une probabilité à 50:50, le rapport entre les deux doit être de 1. Mais il faut faire beaucoup de tirages.
Pour tester notre hypothèse sur le générateur de nombres aléatoires d'App Inventor, nous allons donc simuler un grand nombre de tirages. Pour nous y aider, nous avons l'application Coin Flip Experiment qui va faire des tirages multiples. L'application utilise le bloc entier aléatoire entre 1 et 2. Si le générateur est de bonne qualité nous nous attendons à ce que la probabilité "Pile" et "face" soit à 50:50, donc que le rapport entre les deux nombres soit proche de 1.
Pour que notre hypothèse soit vraie, on doit vérifier que plus le nombre de tirages augmente, plus le rapport entre les nombres de piles et de faces doit être proche de 1 ou 50:50.
Si on le vérifie, cela valide notre hypothèse. Sinon, ça l'invalide.
Téléchargez et installez l'application
Utilisez le scanner de code barre sur votre appareil pour scanner ce QR code, télécharger et installer l'application sur votre smartphone ou votre tablette.
Bien que vous n'en n'ayez pas besoin pour cette leçon, voici un lien vers le code source.
Lecure du code source
Bien que nous venions seulement d'introduire le code source (cf. leçon 4.4), vous devriez être en mesure de lire ce bloc et vérifier si il est valide ou pas. -- c'est à dire de vérifier qu'il effectue N tirage et comptabilise le nombre de cas où le tirage est côté face.
Voici quelques éléments à relever dans le code :
- Il répond à l'évènement BoutonGo.Clic.
- It lit en entrée, une information dansTextBox1.Texte et le stocke dans la variable globale N.
- Avant de faire tout calcul, il vérifie que l'entrée est un nombre entre 1 and 100.
- Il initialise la variable globale Faces à 0. Cette variable est utilisée pour compter le nombre de fois où c'est le côté Face qui sort.
- Il utilise une boucle Pour chaque ... pour faire un tirage à pile ou face N fois.
- Pour chaque tirage il génère un entier aléatoire entre 1 et 2 (bornes comprises).
- Si le tirage est 1, il ajoute 1 à la variable globale Heads (faces)
- Quand la boucle se termine, il affiche les nombres de tirage côté Face et côté Pile.
Activité par groupe ou pour la classe (30 minutes) - méthode POGIL
Constituez des équipes ("POGIL") de 4. Tous les membres de l'équipe doivent télécharger et installer l'application sur leur portable. Enregistrez les réponses en utilisant cette feuille. (Faites une copie pour avoir une version modifiable/éditable.)Donnez à chaque membre de l'équipe un des rôles suivants :
| Rôle | Responsabilité |
|---|---|
| Facilitateur | enregistre les données de l'équipe avec le nombre de tirages et le nombre de faces pour chaque exécution de l'application. Compte les résultats et calcule le pourcentage de faces et de piles. |
| Porte-parole | Rend compte des résultats de l'équipe. |
| Contrôleur qualité | Valide que l'enregistrement des données par le Facilitateur' est correct et vérifie que ses calculs sont justes. |
| Analyste process | Vérifie et enregistre l'avancement de l'équipe et qu'elle est efficace. |
Procédure expérimentale
L'hypothèse à examiner dans cette expérience est que le générateur de nombres pseudo-aléatoires ou PRNG d&39;App Inventor' est un bon modèle de processus aléatoire.
Déroulez les étapes suivantes :
- Faites tourner l'application à plusieurs reprises et notez pour chaque essai le nombre de faces et de piles. Faites le au moins 20 fois. Comme il y a 100 tirages à chaque essai, on aura 2000 tirages après 20 essais de l'application.
- Calculez et écrivez pour chaque essai le pourcentage de faces . Puis calculez et écrivez pour chaque essai la somme des tirages face pour cet essai et des précédents et divisez cette somme par le nombre total de tirage pour avoir un pourcentage cumulé depuis le premier tirage. Par exemple, après le 5° tirage, si les tirages ont donné : 45, 52, 46, 53, 49, le total sera de 245 pour un nombre de tirages égal à 5 x 100. Le pourcentage cumulé sera donc de 245/500 = 0,49 = 49%
-
(Dans votre Portfolio) enregistrez les résultats de votre équipe dans un tableau bien organisé.
Si vous avez fait 20 essais de 100 tirages à chaque fois, votre tableau doit avoir 20 lignes avec le numéro de l'essai, le nombre de tirages pour cet essai, le nombre de résultats 'face', le pourcentage de 'face' pour cet essai, le nombre cumulé de tirages depuis le premier essai et le pourcentage cumulé du nombre de 'faces'.
Voici un exemple:
Cette feuille de calcul peut vous aider à enregistrer vos données. Il suffit d'entrer vos données dans les colonnes B et C. Les autres colonnes seront calculées automatiquement.Essai nb Tirages nb Faces % Faces nb Total tirages nb Total Faces % cumulé Faces 1 100 45 45.0 100 45 45% 2 100 51 51.0 200 93 46.5% - (Dans votre Portfolio) a la lecture de vos résultats pensez vous que le générateur PRNG d'AppInventor est un bon modèle de processus aléatoire ? indiquez les raisons de votre conclusion.
- (Dans votre Portfolio) Un de vos amis affirme que si le résultat de 100 tirages donne un résultat de 45% de faces, c'est que la pièce donne un résultat biaissé ou faussé. Quelle réponse et quels arguments pouvez-vous lui donner ?
Auto-contrôle
Ci-dessous un tableau de termes techniques introduits dans cette leçon. Passez la souris au-dessus pour vérifier leurs définitions.|
modèle PRNG pièce non biaisée hypothèse |
Pour votre Portfolio
Créez une page nommée : PRNG App Inventor dans la catégorie "Réflexions " de votre portfolio, puis faites les travaux suivants et répondez aux questions :
- (POGIL) enregistrez les résultats de votre équipe dans un tableau bien organisé. Si vous avez fait 20 essais de 100 tirages, votre tableau doit avoir 20 lignes de résultats avec le numéro du tirage, le nombre de tirs, le nombre de faces etc. comme indiqué ci-dessus.
- (POGIL) Selon vos résultats, est-ce que le générateur PRNG d'App Inventor est un bon modèle de processus aléatoire ?
- (POGIL) Un de vos amis affirme que si le résultat de 100 tirages donne un résultat de 45% de faces, c'est que la pièce donne un résultat faussé. Ecrivez la réponse et les arguments que vous lui donneriez ?
- Nous utilisons un tirage à pile ou face dans cette expérience, donc nous évaluons la capacité du bloc entier aléatoire entre 1 et 2 d'App Inventor à générer des 1 la moitié du temps. Est-ce que c'est un test suffisant pour évaluer le PRNG d'App Inventor ? Quelles autres expériences pourraient améliorer la confiance dans le PRNG d'App Inventor ?

